Complex Wire Rope .Models for Lifts

by C. Erdönmez1, C. E. İmrak2 and Ö. Salman2
1Turkish Naval Academy, Head of Science Department, Department of Mathematics, Turkey,
2Istanbul Technical University, Faculty of Mechanical Engineering, Mechanical Engineering Department, Turkey

This paper was presented at USA 2012, the ­International Congress on Vertical Transportation ­Technologies, and first published in IAEE book Elevator Technology 19, edited by A. Lustig. It is a reprint with ­permission from the International Association of ­Elevator Engineers (website: www.elevcon.com). This paper is an exact reprint and has not been edited by ELEVATOR WORLD.

Key Words: Wire ropes, modelling, lifts, finite element analysis.

Abstract

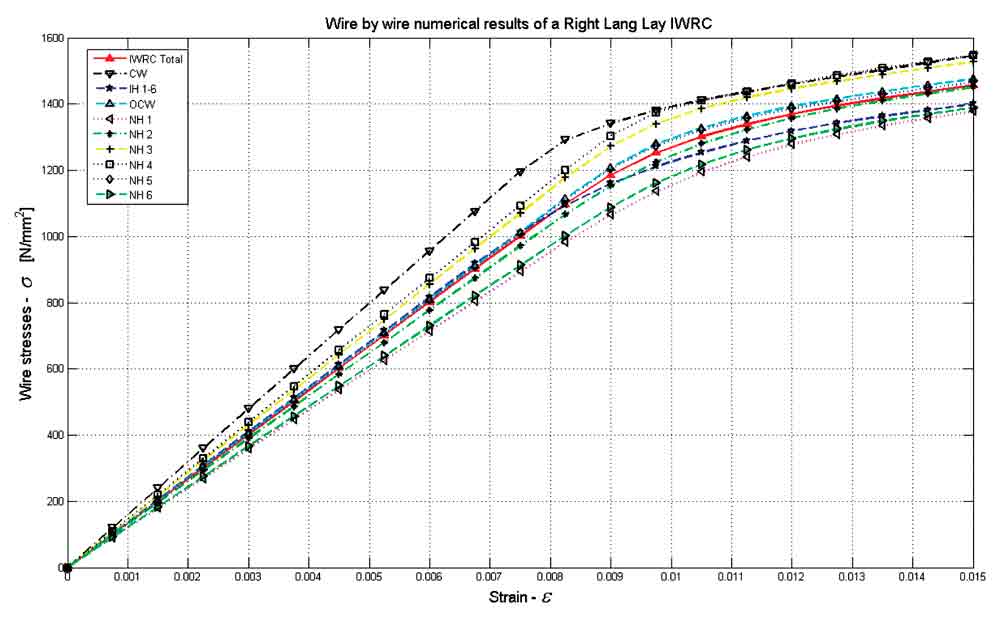
Wire ropes have many practical application areas, some of them are elevators, bridges, lifting systems, mines, cranes etc. Wire ropes are designed using helical shaped wires. Single and double helical wires are used during the modelling issue. A basic part of the wire rope is called strand. An independent wire rope core (IWRC) is built by wrapping wire strands. To model a more complicated wire rope such as Seale IWRC, Seale part is wrapped around an IWRC. In this paper complicated modelling issue for an IWRC is proposed. Numerical models gives opportunity to establish tests over the problems confronted during the applications of wire ropes. The proposed model gives wire by wire numerical results for wires within the specific wire rope model.

1. Introduction

Theory of wire ropes starts with the early studies of Love (Love, 1944). Meanwhile, Costello has gathered general aspects of wire rope theory in his reference book in 1990s (Costello ,1990). Later on Phillips and Costello presented the analysis of internal-wire-rope cores in (Phillips and Costello 1985). A number of papers presented general characteristics of wire ropes are presented in the literature 1980 through 1990 in (Velinsky et.al. 1984, Velinsky 1989). Lately Jiang et.al. mentioned about the finite element model description of simple straight strands in (Jiang et.al. 1999, Jiang et.al. 2000). One of the interesting study on the mechanical behaviour of a wire rope with an IWRC is presented in (Elata et.al. 2004). Analytical procedure for modelling recursively and wire by wire stranded ropes are described and some results for different loading conditions are represented in (Usabiaga and Pagalday 2008). Mathematical and geometrical model and structures are mentioned in (Wang et.al. 1998, Wang et.al. 2002). Lately, Erdönmez and İmrak described geometrical model construction of wire ropes in real 3D manner in (Erdönmez and İmrak 2011, İmrak and Erdönmez 2010).

Tensile strength of wire ropes is one of the important characteristics. Wire ropes have a big number of application areas such as mining, lifting, cranes, railways etc. Classifications of wire ropes are depending on the way of its geometrical design. Its fundamental component is a simple straight wire strand (WS) which is composed by wrapping a straight wire with six single helical wires around. An independent wire rope core (IWRC) is composed by using a WS as a core strand and six outer strands are composed by using both single and double helical wires. IWRC is also used as the core for more complex wire ropes such as Seale and Warrington type IWRCs. In addition, wire ropes are categorized to its lay types. Right regular lay, right lang lay, left regular lay, left lang lay and alternate lay types could be some of the laying types for wire ropes. Lay types for a wire rope are described in Fig. 1. These names are given to the wire ropes depending on the direction of strands and directions of wires within a strand are wrapped throughout.

In this paper a 3-D model generation and axial loading of WS and IWRC is described. Due to its complex shape, wire ropes solid model generation inherent some complex issues. The helical structures of the wires are considered and both single and double helical geometries built in meshed solid forms. First of all meshed geometry of the problem is modelled and the assembled wire rope solid model is brought into Abaqus. Boundary conditions are applied to solve an axial loading problem for WS and IWRC using Abaqus. 8-node reduced integration brick elements are used during the analysis. Both elastic and plastic behaviour of the wire rope is considered with considering the frictional effects. Wire rope analysis using the 3-D computational model gives wire by wire based results. Thus, it is possible to investigate the behaviour and the importance of the each component of the wire rope under the specific loading condition. This analysis methodology can be used for more complicated problems such as wire rope bent over sheave. Due to the complicated geometry of the problem, while the mesh size of the model is increased it needs a huge amount of resource of computer CPU time to solve the problem. For this reason parallel computers are preferred during the solution stage of the wire rope problem.

2. Wire Rope Mathematical Model

Single helical wires are formed by using the general helix equation defined by,

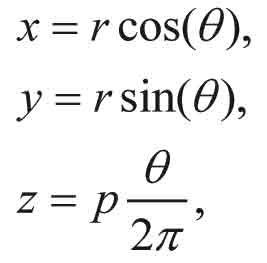
where , r and p represents the turning angle, radius and pitch length of the helix respectively. For the double helical wires the centerline of the core wire is single heli-cal shaped and it is defined by,

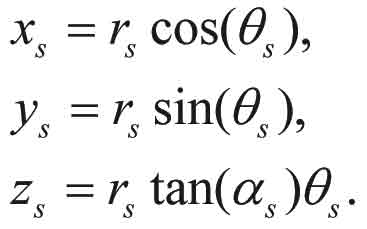
On the other hand the outer six double helical wires are composed by the following equation,

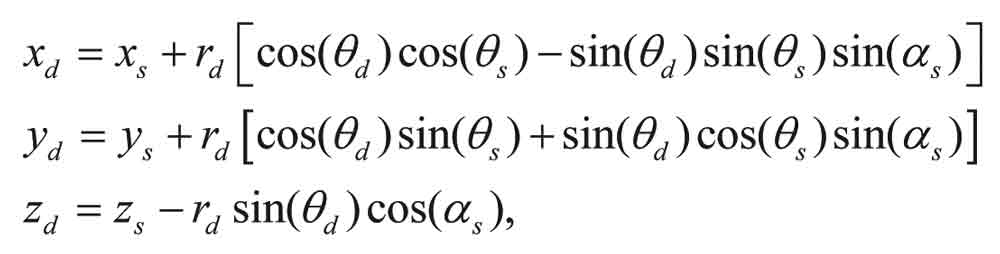
4. Conclusion

In this study a general 3-D model generation issue for wire rope is developed. The generated 3-D model gives opportunity to analyze wire ropes in detail and gives wire by wire based information on wire ropes. Due to these advantages, the proposed numerical model can be used for implementing more complicated problems such as bending over a sheave problem on wire ropes. In addition, by using the developed code, construction of an assembled 3-D wire rope model is accomplished and by the way, time necessary for modeling solid wire rope geometry is cut down dramatically.

REFERENCES
Costello, G.A. (1990). Theory of wire rope. Berlin: Springer.
Elata, D., Eshkenazy, R. and Weiss, M.P. (2004). “The mechanical behavior of a wire rope with an independent wire rope core”, International Journal of Solids and Structures 41:1157-1172.
Erdönmez, C. and İmrak, C.E. (2011). “Modeling Techniques of Nested
Helical Structure Based Geometry for Numerical Analysis”, Strojniški vestnik – Journal of Mechanical Engineering 57, 4, 283-292 DOI:10.5545/sv-jme.2009.006.
Imrak, C.E. and Erdönmez, C. (2010). “On the problem of wire rope model generation with axial loading”, Mathematical and Computational Applications, 15(2):259-268.
Jiang, W.G., Henshall, J.L. and Walton J.M. (2000). “A concise finite element model for three-layered straight wire rope strand.”, International Journal of Mechanical Sciences, 42:63-86.
Jiang, W.G., Yao, M.S. and Walton, J.M. (1999). “A concise finite element model for simple straight wire rope strand”, Int. Journal of Mechanical Sciences, 41:143-61.
Love, A.E.H. (1944). A treatise on the mathematical theory of elasticity. 4th ed., New York: Dover Publications, Chapter XVIII-XIX, pp. 381-426.
Phillips, J.W. and Costello, G.A. (1985). “Analysis of wire ropes with internal-wire-rope cores”, Transactions of the ASME, Vol. 52, 510-516.
Usabiaga., H. and Pagalday, J.M. (2008). “Analytical procedure for modelling recursively and wire by wire stranded ropes subjected to traction and torsion loads”, Internation-al Journal of Solids and Structures, doi: 10.1016/j.ijsolstr.2008.04.009.
Velinsky, S.A. (1989). “On the design of wire rope”, Transactions of the ASME, Journal of Mechanics, Transmissions, and Automation in Design, 111:382-388.
Velinsky, S.A., Anderson, G.L. and Costello, G.A. (1984). “Wire rope with complex cross sections”, Journal of Engineering Mechanics, 110(3):380-391.
Wang, R.C., Miscoe, A.J. and McKewan, W.M. (1998). “Model for the Structure of Round-Strand Wire Ropes”, DHHS (NIOSH), Pub. No. 98-148, Report 9644:1-19.
Wang, G., Sun, J. and Zhang, H. (2002). “Geometric Model and Numerical Simulation For the Laying Process of Wire Rope”, Proc. Int. Conf. on Sci.&Eng. Comp.:407-412.