Electronic Theorems for Design and Repair Professionals

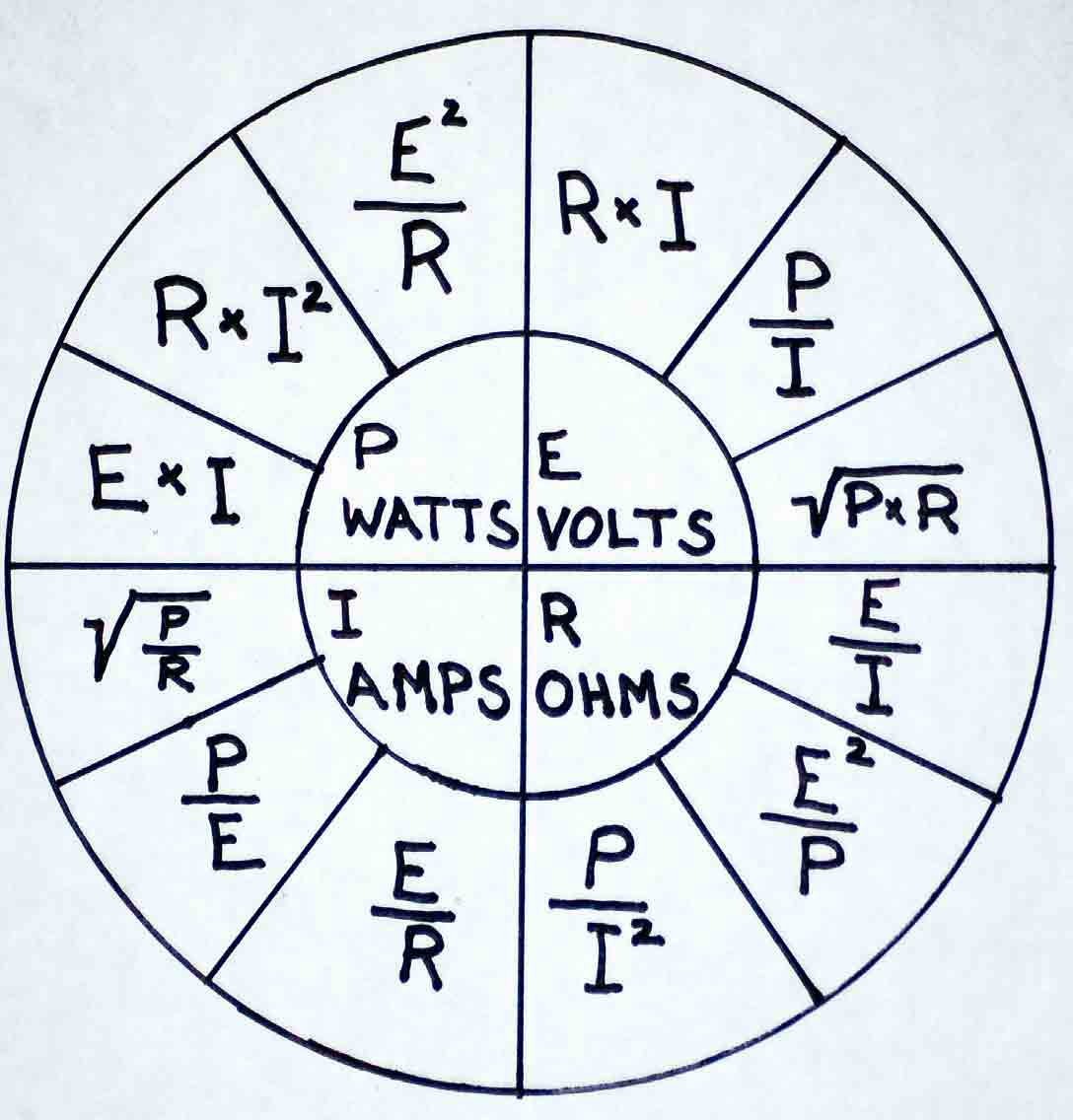
Ohm’s Law Wheel and other important circuit theorems are discussed for practical use.

Virtually all contemporary elevators and escalators are powered by electrical motors, either DC or AC run in conjunction with a variable-frequency drive (VFD). Besides the energy that makes these motors turn, they are also controlled by automatic or manual electric devices. Problems that arise in conjunction with elevators and escalators usually involve the motor or control apparatus, and are more often electrical rather than strictly mechanical.

Learning Objectives

After reading this article, you should have learned about:
♦ Ohm’s Law and derivatives shown in the Ohm’s Law Wheel
♦ Power equations shown in Ohm’s Law Wheel
♦ Use of multimeter functions
♦ Cat 1-4 locations
♦ How electronics technicians use Kirchhoff ’s current and voltage laws

To work with these motor or control systems, designers and repair technicians must have accurate knowledge concerning the activity of all those electrons, and under which conditions and in which direction they are flowing. If measured parameters are not in agreement with circuit requirements, the elevator or escalator will not function reliably, if at all. Acquiring a knowledge of the basic electrical theorems and laws will help an elevator or escalator designer or repair technician make sense of this.

The most frequently used electrical equations are easily accessed by referring to Ohm’s Law Wheel. This elegant graphic contains all Ohm’s Law equations, which relate volts, amperes and ohms. Additionally, the power equations relating volts, amps and watts with derivatives are shown, so you can easily access many equations that are highly relevant when doing electronic design of new systems or troubleshooting an existing faulted unit.

Ohm’s Law, in its most fundamental formulation, is E = I X R, where E = volts (electromotive force), I = amperes (intensity), and R = resistance. The common multimeter can be configured simply by turning the large knob at the center of most models to measure any of these three values. To measure volts, first turn the knob to put the instrument into AC or DC volts mode. Some models have another knob, which is used to set the range. If you do not have a good idea of the approximate voltage to be measured, start at a higher range, and work down to avoid overload. More upscale meters have an auto-range feature. The black probe (in most models) is plugged into “common,” and the red probe is plugged into “volts.” To take a voltage measurement, the two probes are connected to either side of the source or load. (A voltage measurement is always taken by putting the meter in parallel with the source, any in-series device or load.) Since the measurement, by its nature, is taken on a live circuit, great care must be taken to avoid contacting a live wire, terminal or live part of the probe if the voltage is above 12 V. Also, as explained below, the instrument’s category (Cat) rating must be observed.

Resistance measurements are taken on components or circuits that are powered down. The best practice is to unplug the equipment (if it is connected by a cord to a receptacle) or disable the circuit by switching off the correct circuit breaker at the entrance panel, then verifying with a test light (if it is hardwired). Additionally, there is the issue of stored voltage within equipment that is powered down. Capacitors, particularly (but not limited to) high-capacity electrolytics that are part of the power supply, are capable of storing a lethal amount of electrical energy long after the equipment is powered down. Also, there may be distributed capacitance throughout the equipment, so to make resistance measurements, all charge has to be bled out of the equipment before it can be considered not live. This is best done by connecting low-resistance power resistors or other suitable loads at appropriate points, as opposed to grounding out the live terminals with a screwdriver shunted to the chassis.

Like voltage measurements, resistance measurements are taken by placing the probes in parallel with the device or circuit under investigation. If a component is part of a circuit, the resistance reading may be invalid because of parallel resistance that may be present. For this reason, it may be necessary to temporarily take the component out of the circuit, which involves re-soldering it afterward. (To isolate a two-wire component, it is necessary to cut only one of the leads.)

Many multimeters, in resistance mode, also function as continuity testers. To access this mode, turn the function switch to the position that has a musical note icon. If a certain resistance, typically 30 ohms, is not read, the instrument will emit a beep, so quick signal-tracing measurements and checks for short circuits can be performed without looking at the readout. The continuity mode is frequently used by electronic technicians.

In contrast to voltage and resistance measurements, current readings are taken by placing the meter in series with the component or circuit through which current is to be measured. This measurement is, of necessity, done with the equipment powered up. A multimeter is a high-impedance instrument in the volts mode and a low-impedance instrument in the current mode. When a voltage measurement is taken, only a very small amount of current flows through the meter, and that is why a multimeter is capable of reading high voltages. Also, a high-impedance voltmeter will not appreciably load the circuit. In reading current, since it is in series with the component or load, the entire amount of current flows through the meter, which, since it offers little resistance to it, has minimal effect on the operation of the circuit. However, if you read the specifications of your multimeter, you will see that the maximum amount of current permitted in a current measurement is specified. For most meters, it is in the milliamp range. More current will burn up a probe lead, at the least.

Most multimeters have an internal inline fuse that protects the current mode, so if an overload is not too great, the fuse may protect the instrument. Much larger amounts of current can be measured using an electrician’s clamp-on ammeter or an oscilloscope equipped with a current probe. Both of these have magnetic sensing coils that measure the magnetic field surrounding a live conductor, so high-current readings may be taken on a live, insulated wire without cutting into or otherwise disturbing the circuit.

The Ohm’s Law equation cited above is the most fundamental version. From it can be derived R = E/I and I = E/R. The formulae can be found by looking at the Ohm’s Law Wheel, where in all cases, the inner circle is equivalent to an equal sign. Additionally, the Ohm’s Law Wheel depicts the power law P = E X I, where P = power in watts. Derivatives are also shown:

• P = E2/R
• P = R X I2
• I = Square root of (P/R)
• I = P/E
• E = P/I
• E = Square root of (P X R)

Besides watching the range so the meter is not damaged by overvoltage or overcurrent, it is necessary to observe the Cat rating. Instrumentation such as an oscilloscope, spectrum analyzer or multimeter is rated for voltages for each of the four Cat environments. The categories, beginning with Cat 4, which is the most aggressive, are:

• Cat 4, which refers to origin of installation or utility level measurements on primary overcurrent protection devices, and on ripple control units
• Cat 3, which consists of distribution mains that are generally permanently connected to the utility feed, is most frequently found in industrial facilities.
• Cat 2, which consists of local main conductors, is typically found at indoor branch-circuit receptacles. Portable tools and residential appliances fall into this category. For electronic technicians and engineers working at a bench in a laboratory, it is a common category.
• Cat 1, the most forgiving of the four categories, consists of signal-level circuits in electronic (often battery-powered) equipment.

Electronic measuring equipment usually has voltage ratings for the Cat environments that are appropriate to the unit printed on one of its panels. For example, an oscilloscope at the analog inputs may be marked “Maximum 300 Vrms Cat 2,” and this limit should be scrupulously observed.

As we have seen, there are many electronic equations that can be accessed at a glance from the Ohm’s Law Wheel. A quantity within the inner circle should be placed on the left side of the equal sign, and it becomes the unknown, which is to be found by calculation. This involves a modest amount of number crunching, readily performed by means of a hand calculator.

In troubleshooting existing electrical equipment, E appearing on the left as an unknown is not frequently used, because the utility voltage is a given, and power-supply voltages, if there is uncertainty, can be picked up off the schematic. In designing new equipment, it’s a different story. This form of the equation might be useful if one wanted to design a power supply that could be connected to predetermined load to attain a desired amount of current. In this connection, recall the definition of a volt: the unit of electromotive force that will drive 1 amp of current through 1 ohm of resistance. It is important to realize that this metric is not time related. It is ongoing, existing at a level that relates to the current and resistance. Even in an AC circuit where it is fluctuating at a constant or varying rate, it is what it is, on an instant-by-instant basis.

Moving clockwise around the Ohm’s Law Wheel, the next variable to be encountered is resistance, expressed in ohms. Given that you know the voltage and can measure the current, resistance can be easily calculated if you don’t want to break open or power down a circuit to measure it.

Continuing clockwise around the Ohm’s Law Wheel, the next quantity that can be made to stand alone on the left side of an electronic equation is I, which denotes current in amperes (or, very often, milliamps, thousandths of an amp). It originally stood for intensity, which is how early researchers visualized current. The equation that can be solved for I is a very useful form of Ohm’s Law, because current in amps is often not known. It can be calculated from the equation, and the result can be compared to the measured value. This will provide valuable information about what is going on in a circuit, stage and the overall equipment.

Power equations, while not strictly speaking a part of Ohm’s Law, are usually included in the Ohm’s Law Wheel, and this adds immensely to its functionality. Experienced electronic technicians and engineers quickly learn to think in terms of power, and then, a lot of things become clear.

Voltage exists at the terminals of a power source and is applied to a load. There is voltage but no current at a switch when it is off. Current flows through a load and varies with the load. Voltage at the terminals of the source is constant, regardless of the load, unless the source is a high-impedance (relative to the load) source, in which case the voltage drops because it is overloaded. This is what happens when a gasoline-powered generator slows down when a heavy load goes online.

Current flows through a load. It is constant everywhere in a circuit unless there are parallel branches or leakage to ground. In any case, current flowing through alternate paths can be added to construct a straight-line path. Then, the current is the same throughout the circuit, including within the source and load.

Power is the product of current and voltage. Current flows from the source through the load and returns via a second conductor to the source. Power is more appropriately visualized as being transferred from the source to the load, where it is dissipated. It can be accurately represented by means of a one-line diagram.

Among the equations contained in the Ohm’s Law Wheel, one of the most important is P = I2 X R. Power is generated in the source and transferred to the load(s), where it is dissipated. It does not return to the source. The amount of power, in watts, consumed by the load is equal to the square of the amount of current in amperes that flows through the load, times the resistance of the load in ohms. (This refers to a DC circuit. The same dynamics apply in an AC circuit, but it can become a little more complex due to the presence of capacitive and inductive reactance, which are added vectorially to the resistance to comprise impedance. Like resistance, this is measured in ohms and conforms to Ohm’s Law, but it is derived differently.)

Since I is squared, it is a far more important factor in making up P than R is. Electronic engineers speak of I2R energy dissipation. To take a simple example, when current passes through a resistor, the same current that enters the resistor leaves it. That amount of current is the same throughout the circuit. Since power does not return to the source, it must go somewhere else. The fact is that it either remains in the load where it is stored, is temporarily stored outside the load as in a magnetic field, or is dissipated in the form of heat and/or information. The troubleshooting process is greatly facilitated by looking at the power generated at the source and asking where it goes.

The generic form of the power equation is P = E X I, or, as it is usually stated, “volts times amps equal watts.” Current and voltage are equally significant factors in determining power. If power remains constant, voltage and current have an inverse relationship. The water analogy is sometimes useful; if we equate current flowing through an electrical conductor to water flowing through a pipe, some comparisons can be made. Voltage is like water pressure, and current is like water flow, which may be expressed as gallons per minute. Electrical resistance, as when the cross-sectional area of a conductor is reduced, is like substituting a smaller-diameter water pipe. A capacitor is like a rubber membrane placed in the water pipe so that oscillations or single pulses can be transmitted, but a continuous flow is blocked. An inductance is equivalent to an expansion tank tee’d off the main line. A water system that will simulate the behavior of a diode; transistor; or, in principle, any type of integrated circuit or microchip can be constructed.

There are numerous electronic theorems not illustrated in the Ohm’s Law Wheel. Two very important circuit theorems are Kirchhoff’s current and voltage laws. They were first stated by the German theoretician Gustav Kirchhoff in 1847, generalizing Ohm’s law and laying the foundation for the work of James Clerk Maxwell, who formulated his classical theory of electrodynamic radiation in 1865, demonstrating that electricity, magnetism and light are manifestations of the same phenomenon.

Kirchhoff’s Current Law (KCL) states that the amount of current going into any circuit node is equal to the amount of current going out of that node. If we stipulate that the current leaving a node is equivalent to the negative amount of the current entering it, the sum of those currents is zero. Kirchhoff’s Voltage Law is closely related. It states that, in an electrical circuit, the sum of the voltages around any closed loop is zero.

These laws, taken together, provide the electronic technician with a useful tool for anticipating correct voltage and current readings that will appear at various points in an electrical circuit.

Thévenin’s Theorem was stated by Hermann Von Helmholtz in 1853 and reformulated in its present form 30 years later by Léon Charles Thévenin. It is widely used to simplify complex circuits having multiple voltage and current sources. Even though these circuits conform to Ohm’s Law, in many cases, the calculations are very difficult going this conventional route. Thévenin’s Theorem, along with its close relation, Norton’s Theorem, permits us to regard the circuit as a black box that can be converted to a Thévenin-equivalent circuit.

The only problem, then, is to construct a valid equivalent circuit that will provide the correct numbers. This equivalent circuit will contain two virtual devices that are in series, a resistance represented as Rth and a voltage represented as Vth. First, replace all voltage and current sources with their internal resistances. An ideal voltage source will be replaced by a short circuit. An ideal current source will be replaced by an open circuit. (This method works only when the sources are independent from each other.)

Another very significant theorem for providing insight into the inner workings of electrical circuitry is the Maximum Power Theorem. It states that maximum power is transferred from a source to a load only when their impedances are equal. This sounds somewhat counterintuitive at first. After all, how can maximum power be transferred to a load that has an impedance that is above zero? The explanation is simple. The way to understand the Maximum Power Theorem is to keep in mind that voltage times current is equal to power. So, if the impedance is greater in the load, the flow of current is reduced, resulting in lower power transfer. Similarly, if the impedance is less in the load, the voltage from the source is reduced, because more of it will appear across the source impedance. This also results in reduced power transfer. The greatest power transfer would occur when both impedances were equal to zero, but, of course, this would be a catastrophic short circuit.

Impedance matching is very important in many applications, from very small traces on a circuit board to huge high-voltage power lines.

In addition to maximum power transfer, in data transmission, impedance matching of source, load and transmission line such as coaxial cable or Cat 5e unshielded twisted pair is essential to prevent harmful data reflections from the load or cabling back to the source. These reverse-direction reflections result in data collisions, causing signal corruption and loss of information.

The strange thing about impedance matching is the matter of characteristic impedance of the transmission line. Coax and other types of data cable are manufactured to have a specific characteristic impedance, expressed in ohms. This characteristic impedance is constant for the type of cable, regardless of the length of the run. It cannot be measured at one end of the line with an ohmmeter, regardless of whether the two connectors at the far end are shunted together.

Characteristic impedance works as it does because it is composed of parallel capacitance and series inductance, both of which increase with length. These metrics oppose one another, making for a constant characteristic impedance independent of length.

Wiring layout is crucial to avoid impedance mismatches when designing chassis wiring and circuit-board traces, especially at high frequencies. For this reason, when repairs are made, it is essential to observe the original conductor lengths, wire type and routing so as not to disrupt the characteristic impedances incorporated in the original design.

Although off-topic for an article on electronic theorems, it should be mentioned that in any wiring changes made during a repair, observe temperature ratings of the original conductors, especially when they pass close to a potential heat source, such as a large transformer or heating element.

Learning-Reinforcement Questions

Use the below learning-reinforcement questions to study for the Continuing Education Assessment Exam available online at www.elevatorbooks.com or on p. 187 of this issue.
♦ What are the two types of laws shown in Ohm’s Law Wheel?
♦ Why do electronics engineers speak of I2R loss?
♦ What are the four Cat locations?
♦ How do Kirchhoff ’s laws help electronics technicians verify that a circuit is working correctly?
♦ Why should source, line and load impedances match in a digital data circuit?