Reducing Energy Consumption by an Optimization Algorithm in Elevator Group Control

by Anton Glad, Juho Kokkala, Mirko Ruokokoski, Janne Sorsa and Toni Tukia

This paper was presented at the 2022 International Elevator & Escalator Symposium in Barcelona, Spain.

Abstract

An elevator group controller (EGC) is responsible for allocating calls given by passengers to be served by elevators. Modern EGCs pick the best elevator for each call by optimizing some objective function, such as the average waiting time or average time to destination of the passengers, or a combination of those.

Due to climate change mitigation initiatives, interest in energy efficient solutions is expected to increase. More generally, future EGCs need to be able to balance between service quality provided to passengers and resource consumption. These two aspirations are typically conflicting as, for example, reducing the amount of energy spent may require increasing the waiting times or times to destination of some passengers. To balance between these objectives, the EGC should adapt to the traffic conditions so that energy can be saved during low passenger demand, while the service quality provided to passengers during high demand and handling capacity are not sacrificed. One approach for this is to adjust weight parameters describing the relative importance of the various objectives in the objective function, such that the achieved service quality matches some target. Ideally, it should also be possible to adjust the importance of energy saving based on the needs of a particular building.

The purpose of this paper is to demonstrate a recently developed, elevator group control algorithm that handles the tradeoff between service quality and energy consumption by changing the weights of the objectives, attempting to ensure adequate service quality during all times while enabling energy savings during periods of low demand. To study the performance of the new algorithm with people flow simulation, we simulate a set of cases considering different elevator group sizes, different traffic conditions, as well as both conventional control and destination control systems.

1. Introduction

Energy consumption and the efficient use of natural resources have become ever more critical as we are evidencing climate change and experiencing an energy crisis. Therefore, all means should be fully utilized in reducing both embodied carbon, as well as operational energy consumption. The building sector accounts for approximately one-third of the total energy consumption in the world.^[1] Elevators are estimated to consume 1% of the total electricity consumption in developed countries, with large variance between buildings.^{[2, 3]}

During peak traffic, elevators can account for up to 40% of the total power demand in a tall building.^[4]

Planning and selection of passenger elevators for high-rise buildings relies on the principle that an elevator installation should satisfy peak passenger demands.^[5] Ideally, an elevator installation does not have slack capacity during peak hours. Outside the peak hours, however, energy consumed by elevators could be reduced by control means (e.g., [6, 7, 8]).

This paper introduces a new energy-saving EGC. It comprises a multi-objective optimization algorithm to allocate passenger calls to elevators and a method to adapt weight coefficients between conflicting optimization objectives, namely passenger service quality and energy consumption. While the method has been developed for all kinds of control systems, energy-saving potential depends on what information a control system can provide to its call allocation and how it can adapt to changing traffic conditions.

A conventional control system (CCS) only registers traveling directions of passengers via up and down call buttons on each landing and destinations via floor selection buttons in elevators.^[5] Therefore, call allocation has limited information about passenger demand to optimize elevator routes. However, CCS typically allows the reallocation of calls, which enables the system to adapt to changing passenger demand.^[9]

On the other hand, a destination control system (DCS) requires each passenger to select a destination floor already at the lobby but immediately allocates a given call to an elevator.^[10]
A hybrid DCS introduces up-and-down call buttons on upper floors, where calls can be reallocated as in a CCS.^[11] However, an advanced destination control system (ADCS) collects passenger destination floors at all lobbies but, at least on upper floors, delays the allocation of calls until the serving elevator starts decelerating to the landing.^{[12, 13]}

To quantify reductions in elevator energy consumption by the new optimization algorithm in both conventional and destination control systems, typical daily passenger demands are simulated with Building Traffic Simulator (KONE BTSTM).^[14]

The rest of this paper is organized as follows. Section 2 discusses modeling of elevator energy consumption. Section 3 describes the new EGC based on multi-objective call allocation that optimizes both passenger service quality and elevator energy consumption. Section 4 defines a simulation method for evaluating energy consumption based on a typical daily passenger demands. Section 5 reports simulation results while Section 6 concludes the paper.

2. Modeling of Energy Consumption

Operational energy consumption of an elevator is dictated by the applied elevator technology and elevator usage, i.e., group control logic and passenger demand. Commonly, the energy consumption is divided into running and non-running energy.^[15] Running energy includes all energy consumed during elevator movement and door operations. The non-running energy is typically divided into idle and standby periods. Idle periods include the time when the doors are open and users enter and exit the car, and the time the doors are closed in idle mode. A standby period starts when the elevator goes into deep energy saving mode, typically after 5 min of inactivity.

This study utilizes elevator designs typical to the buildings analyzed in this paper. Energy consumption for the elevator movement, i.e., hoisting energy, includes such design aspects as the employed machinery and drive type, mechanical components used in the machinery bedplate and the shaft, as well as the masses of the counterweight, elevator car, and suspension and compensation ropes.

Besides the applied elevator technology, the dynamics and kinematics of each trip affect the energy consumption of the trip. The most dominant factors include loading, the direction of movement and the distance of the trip. Additionally, the applied speed, acceleration and jerk values influence the energy losses in the machinery and shaft.

In addition to the energy consumed by the hoisting operations, each electrical component and sub-system in the elevator can also be modeled to have certain power demand characteristics that depend on the operation mode of the elevator: running, door operations, idle and standby. Combining the energy consumption details of the electrical and hoisting model, one can calculate the energy consumption for each trip the elevator takes as well as the energy consumed in the idle and standby modes.

3. Energy-Efficient Group Controller

An EGC decides which elevator serves which call and in which order the calls are served. A common method to solve this dynamic online problem is to solve a sequence of snapshot problems, where at each decision point, all current calls are allocated given the information currently available. The objective function in the snapshot problem usually comprises only passenger service quality measures, e.g., average waiting time or average time to destination of the passengers. The snapshot problem is solved, e.g., using genetic algorithms. See, e.g., [16, 12].

Tyni and Ylinenconsidered adding energy consumption to the objective function.^[7] During low passenger demand, it is possible to save energy by making call allocation decisions that are worse in terms of service quality while better in terms of energy consumption. During high demand, there is less room for saving energy as the cost paid in passenger service quality may be too high. Thus, the relative weights of these objectives need to be adjusted based on the demand. For this, they present an approach for a CCS where a proportional-integral-controller (PI-controller) is used to adapt the relative weights of call time of landing calls and energy consumption, with the aim of maintaining the average call time at a specific target level.^[7]

In the case of a DCS, there is a known need to adapt the relative weights of e.g., waiting time versus transit time or time to destination based on traffic situation, as during high passenger demand, time to destination optimization is needed to maximize handling capacity while during lighter demand a preference for minimizing waiting time can be taken into account (e.g., [14]). To consider energy consumption in the DCS in addition to passenger service quality, the EGC needs to adaptively change weights of three objectives, namely, waiting time, transit time, and energy consumption.^{[17, 12]}

This paper proposes a group controller algorithm that balances between waiting time (WT), transit time (TT) and energy consumption (EC). The snapshot optimization problem is of the form

min_𝑥 : Σ_𝑖∈𝑃 𝑊𝑇_𝑖(𝑥) + 𝜔^WTΣ_𝑖∈𝑃 𝑇𝑇_𝑖(𝑥) + 𝜔^EC𝐸𝐶(𝑥) + 𝑝(𝑥)

where 𝑃 is the set of passengers, 𝑥 is the call allocation solution, 𝑊𝑇_𝑖(𝑥), 𝑇𝑇_𝑖(𝑥) are the WT and TT of passenger 𝑖 if 𝑥 is selected, 𝐸𝐶(𝑥) is a measure of the energy consumption cost caused by the solution 𝑥, and 𝑝(𝑥) contains other terms. Finally, 𝜔^WT, 𝜔^TT, and 𝜔^EC are weight coefficients controlling the relative importance of the three objectives.

Extending the PI-controller approach,^[7] two separate target levels are defined, one for average waiting time (AWT) and one for average transit time deviation (ΔATT), the difference between transit time and an ideal transit time without stops and other delays. This ΔATT is used because it depends less on the number of traveled floors and, thus, nicely generalizes to all kinds of elevator groups.

For both targets, a separate PI-controller is introduced. Each controller is monitoring one target quantity, outputting a control signal, denoted by 𝑢^TT, 𝑢^WT ∈ [0,1], respectively. Each controller increases the control signal if the observed level of the corresponding quantity is above target level and decreases the control signal if the observed level is below target. The observed level is here formed by exponential smoothing of results of the snapshot problems, similarly to^[7].

𝜔^TT = (𝑢^TT + (1 − 𝑢^TT)𝑢^WT),
𝜔^TT = 𝑢^TT ,
𝜔^TT = (1 − 𝑢^TT)(1 − 𝑢^WT).

Finally, the control signals of the two independent PI-controllers need to be combined into weights for the objectives. For DCSs, if the ΔATT target is not met, all focus should be on maximizing the handling capacity of the group. When the ΔATT target is met, there is room for considering other preferences – keeping AWT at the desired level and reducing EC. The weights obtained from the control signals should therefore i) approach pure time to destination optimization whenever 𝑢^TT approaches 1 (ΔATT above target), ii) approach pure waiting time optimization when the control signal (𝑢^TT, 𝑢^WT) approaches (0,1), iii) approach pure EC optimization when both control signals approach 0. These desiderata are fulfilled by the following mapping:

For CCSs, the same approach with two targets and corresponding controllers is used, but the relative weighting between WT and TT is kept fixed. In this case, the weights are otherwise as above, except 𝜔TT is instead set to 𝑤(𝑢^TT + (1 − 𝑢^TT)𝑢^WT), where 𝑤 is a constant controlling the tradeoff between WT and TT.

4. Simulation Method and Performance Indicators

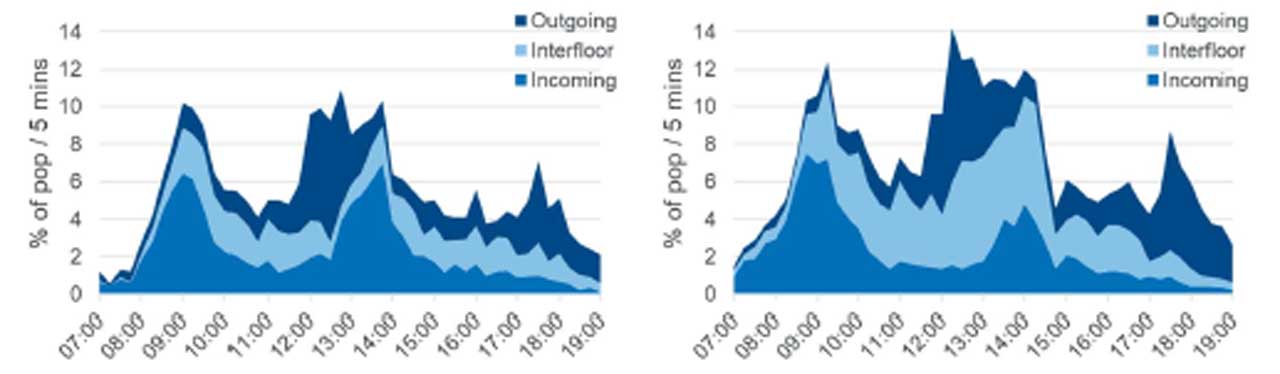
ISO 25745-2:2015^[15] and VDI 4707-1:2009^[18] introduce methods to estimate energy efficiency of elevators. Both are based on a fixed number of elevator trips and meant to be applied to single elevators. However, to assess the effect of a control system on energy consumption and to compare different technologies, a simulation method is needed in the evaluation. Daily passenger demands based on measurements in a multi-tenant and in a single-tenant office, as illustrated in Figure 1 are simulated.^[9] Elevator trips occuring in the simulations are associated with running energies modeled per specific load and travel distance, which enables the calculation of the daily running energy consumption.^[15]

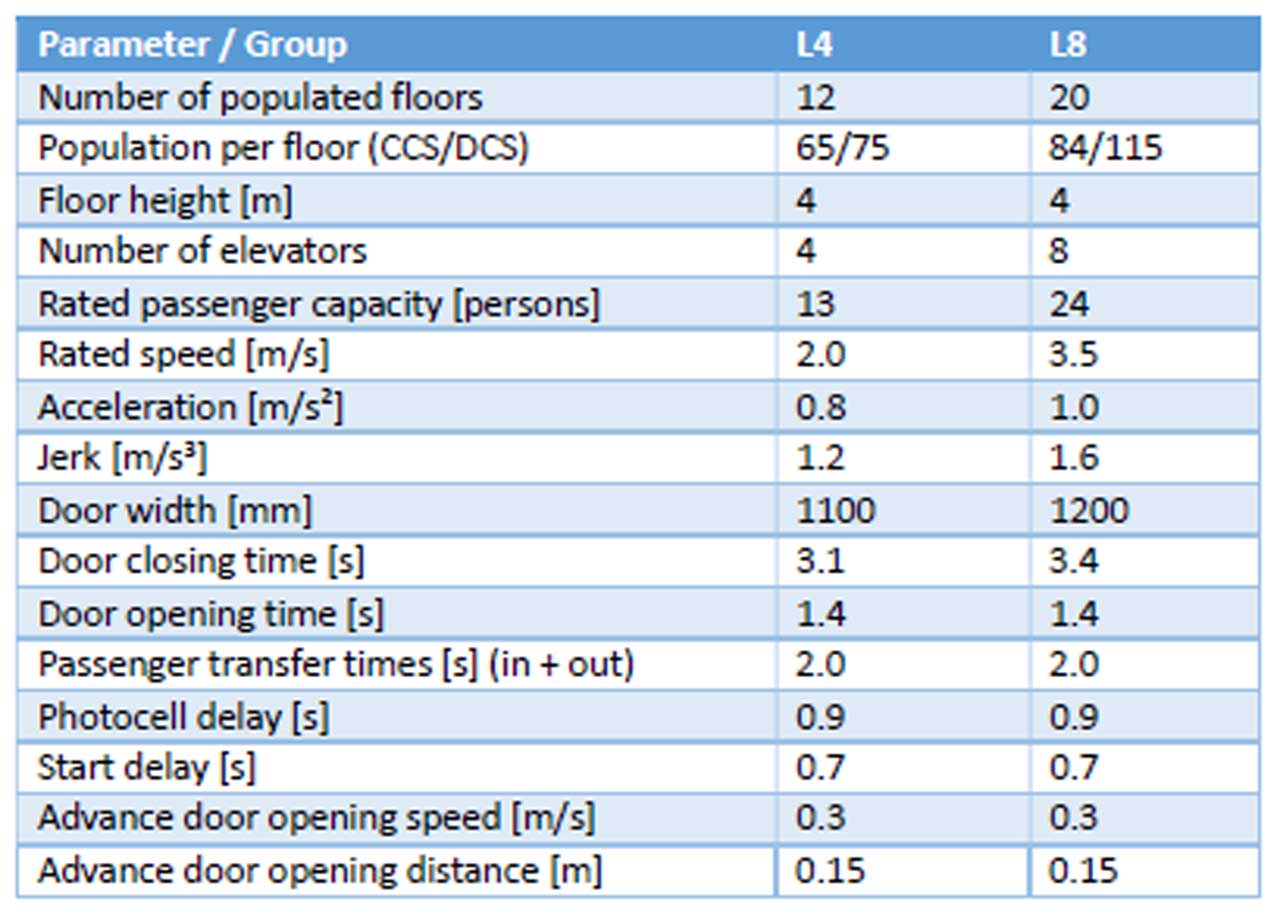
Two different elevator groups are considered, named L4 and L8. Elevator and building parameters are shown in Table 1. Both CCSs and DCSs are considered. The elevator group parameters are selected in such a way that CCS groups have at least a handling capacity of 12% of population per 5 min.^[5] The DCS groups have larger populations than the corresponding CCS groups, which decrease their handling capacities to about 10% per 5 min when calculated with standard formulas. Thus, the DCS groups in this experiment are required to boost handling capacity during up peak traffic and are generally under heavier passenger demand compared to the CCS groups.

To assess the effects of energy-efficient group controls, the following key performance indicators (KPI) are used:

• Average waiting time (AWT)^[5]
• Average transit time deviation (ΔATT), defined in Section 3
• Average time to destination (ATTD)^[5]
• Number of elevator starts
• Running energy consumption (EC), the sum of energy consumptions over elevator trips, including door operations.
• Running energy consumption per load and distance (ECPLD)^[19]
• Car Load Factor (CLF), the maximum number of passengers as a percentage of rated passenger capacity during an elevator round trip, averaged over round trips.
• Intermediate stops (IS), average number of stops that a passenger faces during their journey, excluding stops at the origin and destination floors.

5. Simulation Results

In the following results, to reduce variance, the simulations were repeated with three independent realizations of random passenger arrivals, and the results reported are averages over them.

5.1 Simulations With Destination Control Systems

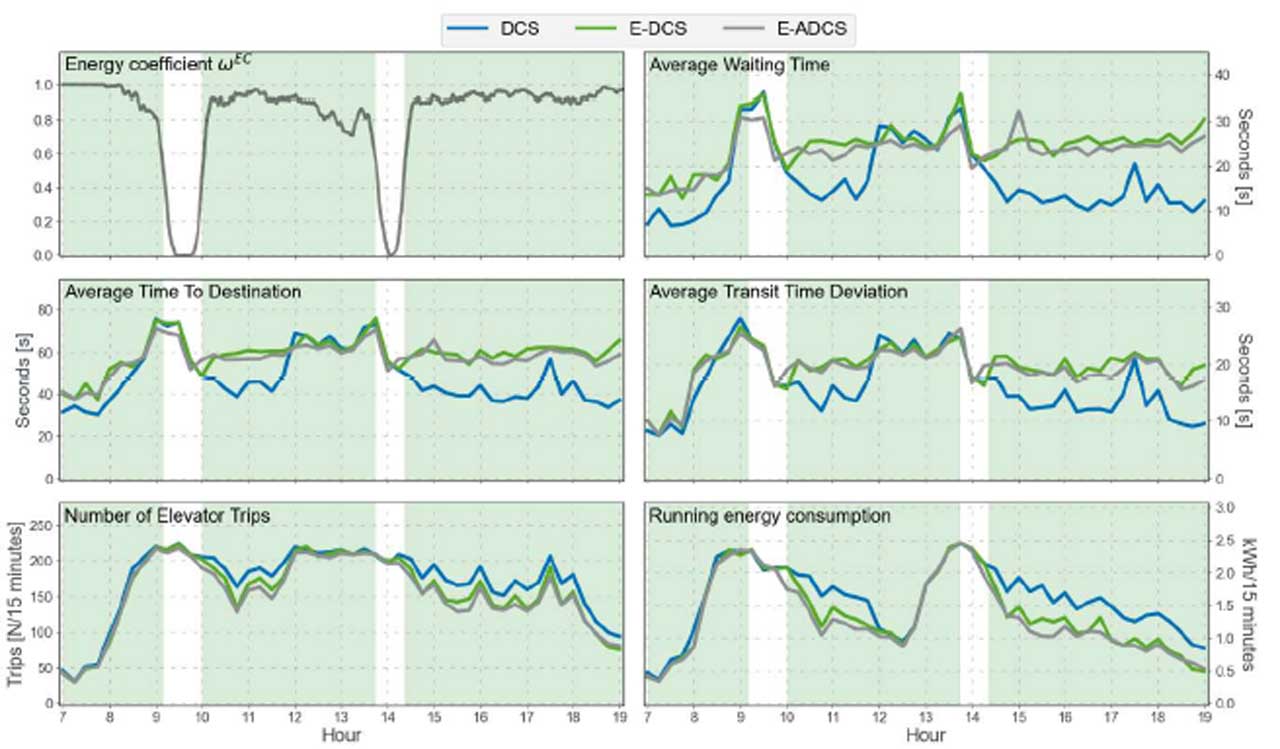
Figure 2 shows the results of simulations with daily passenger demand in a multi-tenant office for elevator group L4. Three destination control systems are considered. DCS (blue line) allocates passenger calls by considering only service quality, E-DCS (green line) and E-ADCS (grey line) are based on the new multi-objective optimization controller, which also considers elevator energy consumption. DCS and E-DCS allocate calls immediately after they are registered, while E-ADCS delays the allocation on upper floors. The following metrics are plotted as a function of time: energy coefficient 𝜔^EC from the first realized E-ADCS simulation, AWT, ATTD, ΔATT, EC, and the number of elevator trips. The green background indicates when the energy weight coefficient is above 0.5, which can be interpreted as a rough indication of when the group controller aimed at saving energy.

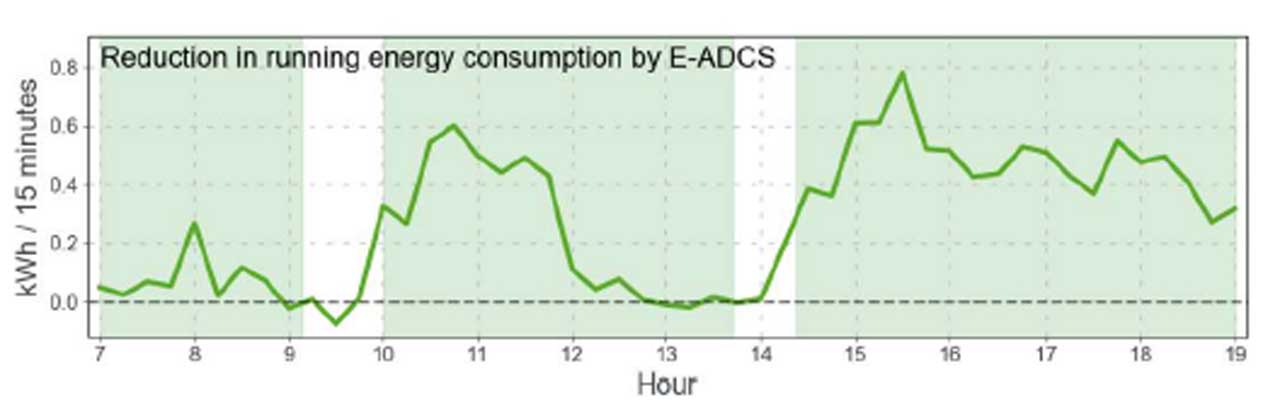
The results show that, on average, waiting times and times to destinations of E-DCS and E-ADCS increase during off-peak hours to save energy. Nevertheless, average waiting time and average transit time deviation remain close to their target levels, 25 s and 20 s, respectively. The number of elevator trips, however, decreases, as more calls are allocated to the same elevators. The energy saving is most prominent when outgoing traffic is dominant. This can be verified from Figure 3, which shows the reduction in running energy consumption by E-ADCS compared to DCS. Outgoing traffic happens, for example, at around 11 a.m. when the lunch time begins and during the whole afternoon after 2 p.m.

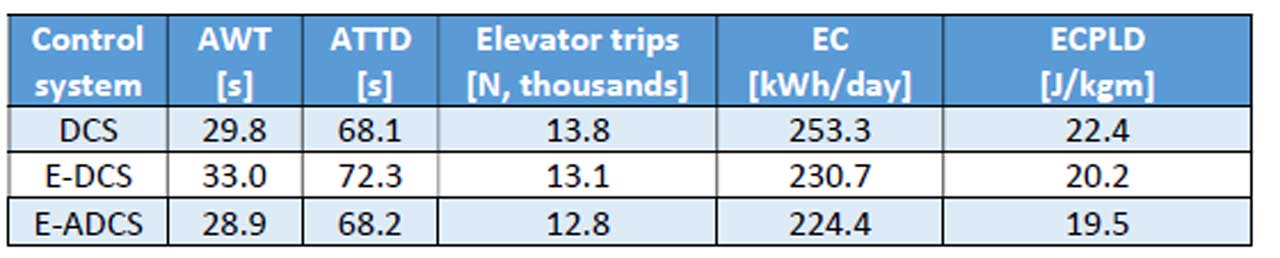
Table 2 reports the averages of some KPIs in the aforementioned simulation. In this case, E-ADCS reduces the number of trips by 10% and running energy consumption by 18%.

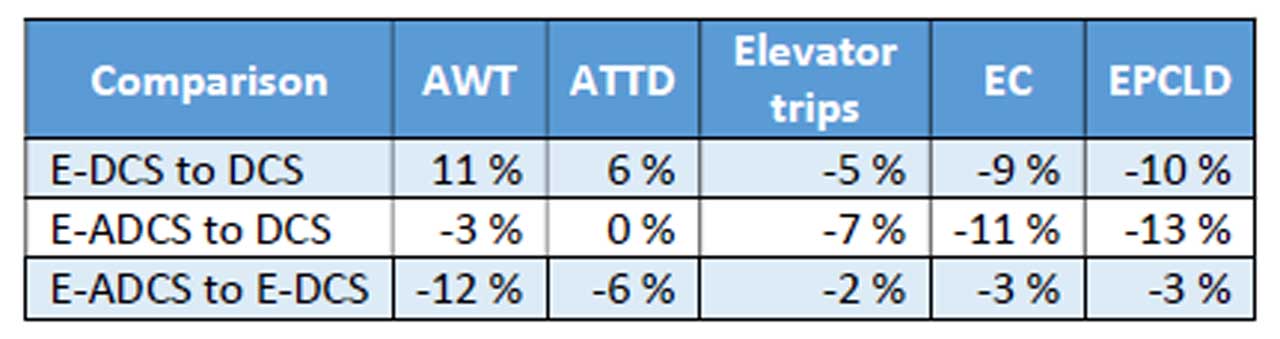
Table 3 shows the average KPI values over both elevator groups and demand profiles, where the average over each individual simulation was first calculated. Table 4 shows a comparison of these results between the different control systems. The results demonstrate that, by using the energy efficient group control, running energy consumption was reduced on average by 9% with E-DCS and 11% with E-ADCs. The number of trips was also reduced by 5% and 7% respectively, possibly contributing to less frequent need for maintenance. However, the tradeoffs of energy saving with DCS are 11% longer AWT, as well as 6% longer ATTD. Using E-ADCS can save even more energy while at the same time achieving shorter waiting times and times to destinations, as well as fewer elevator trips throughout the day.

5.2 Simulations With Conventional Control Systems

The simulations were also conducted with CCS. Table 5 shows the results of these simulations, where the control system CCS refers to call allocation by the full collective control principle and E-CCS to call allocation based on the new optimization algorithm. The results are averages over the two group sizes and two traffic profiles. The improvements of using E-CCS compared to CCS are shown in the last row. With CCS, the biggest tradeoffs of energy saving happen to CLF and IS metrics.

6. Conclusions

In this paper, an elevator group control algorithm optimizing both passenger service quality and elevator energy consumption was presented. The group control allocates elevators to passenger calls with a multi-objective optimization algorithm that balances between passenger service quality and elevator energy consumption by using weight coefficients balances between. In addition, the group control adjusts the weight coefficients service quality to preset target values. To compare energy consumption between control systems, a simulation method was proposed. Simulation of daily passenger demands provides exact data on elevator trips, i.e., the number of trips with a particular travel distance and a particular number of passengers. The daily running energy is then calculated as the sum of elevator running energies of all elevator trips, where the trip-wise running energy may be based on either modeling or measurements.

The effect of the new group control on service quality and energy consumption was demonstrated by simulation experiments on hypothetical office buildings. The new optimization algorithm in a conventional control system resulted in a saving of 17% in elevator running energy and in a reduction of elevator starts by 6%. In the case of destination control systems, running energy was reduced by 9% with a traditional destination control with immediate call allocations, and by 11% with the new advanced destination control that allows the reallocation of passenger calls on upper floors. It is worth noticing that the DCS simulations were conducted with clearly higher passenger demands than the simulations with the CCS. Due to the capability of transporting more passengers, running energy consumption per passenger with DCS was lower than with CCS. Furthermore, ADCS with the new optimization algorithm provided as high as 30% reduction in running energy consumed per load per distance compared to the CCS with full collective call allocation.

Thus, the best potential in reducing elevator running energy arises from the control system that collects detailed data on passenger journeys and leaves enough flexibility to adapt to the evolving traffic conditions. The new optimization algorithm can be expected to provide significant energy savings not only in offices but also in other kinds of buildings, where elevator groups are well planned and elevators are not operating at their performance limits all the time. Furthermore, elevator standby modes provide further savings in energy consumption. Their effect on the total energy consumption can also be incorporated in the simulation model, along with the energy consumed during idle periods, and included when reporting life-cycle consumptions and CO₂ emissions.

References

[1] International Energy Agency (IEA), ”World Energy Outlook,” IEA, Paris, 2021.

[2] T. Tukia, S. Uimonen, M.-L. Siikonen, C. Donghi and M. Lehtonenn, “Modeling the aggregated power consumption of elevators – the New York city case study,” Applied Energy, vol. 251, p. 113356, 1 October 2019.

[3] A. De Almeida, S. Hirzel, C. Patrão, F. Joäo and E. Dütschke, “Energy-efficient elevators and escalators in Europe: An analysis of energy efficiency potentials and policy measures,” Energy and Buildings, vol. 46, pp. 151-158, April 2012.

[4] K. Al-Kodmany, “Tall buildings and elevators: A review of recent technological advances,” Buildings, vol. 5, no. 3, pp. 1070-1104, 2015.

[5] ISO, ISO 8100-32:2020 Lifts for the transportation of persons and goods — Part 32: Planning and selection of passenger lifts to be installed in office, hotel and residential buildings, Switzerland: International Organization for Standardization, 2020.

[6] R. Peters, “Green Lift Control Strategies,” International Journal of Elevator Engineers, vol. 2, 1998.

[7] T. Tyni and J. Ylinen, “Evolutionary bi-objective optimisation in the elevator car routing problem,” European Journal of Operational Research, vol. 169, no. 3, pp. 970-977, 16 March 2006.

[8] S. Kobori, M. Iwata, N. Suzuki and S. Yamashita, “Energy-Saving Techniques of Elevator Group Control System,” in Elevator Technology, 2010.

[9] M.-L. Siikonen, ”Planning and Control Models for Elevators in High-Rise Buildings,” Doctoral dissertation, Helsinki University of Technology, 1997.

[10] J. Schröder, “Advanced dispatching – destination hall calls + instant car-to-call assignment: “M-10”,” Elevator World, vol. 38, no. 3, pp. 40-46, March 1990.

[11] M.-L. Siikonen, J. Sorsa and T. Susi, “KONE Polaris Hybrid,” Elevator World, vol. 60, no. 7, pp. 108-112, July 2012.

[12] J. Sorsa, “Optimization Models and Numerical Algorithms for an Elevator Group Control System,” Doctoral dissertation, Aalto University, 2017.

[13] R. Barker, “Harmonized Elevator Dispatching and Passenger Interfaces,” Elevator World, vol. 66, no. 11, pp. 82-90, November 2018.

[14] M.-L. Siikonen, T. Susi and H. Hakonen, “Passenger traffic flow simulation in tall buildings,” Elevator World, vol. 49, no. 8, pp. 117-123, August 2001.

[15] ISO, ISO 25745-2:2015 Energy performance of lifts, escalators and moving walks — Part 2: Energy calculation and classification for lifts (elevators), International Organization for Standardization, 2015.

[16] T. Tyni and J. Ylinen, “Genetic Algorithms in Elevator Car Routing Problem,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001), San Francisco, 2001.

[17] T. Hautamäki, “Multiobjective Optimization Model for Elevator Call Allocation,” Master’s thesis, Aalto University, 2021.

[18] VDI, VDI 4707:1 Aufzüge Energieeffizienz, Düsseldorf: VDI Verein Deutscher Ingenieure e.V., 2009.

[19] A. So, G. Cheng, W. Suen and A. Leung, “Elevator Performance Evaluation in Two Numbers,” Elevator World, vol. 53, no. 1, pp. 102-105, 2005.

Acknowledgments

This research is co-funded by Business Finland Veturi funding under the Flow of Urban Life program.