Introduction
by Zhu Lin, Jiang Qing, Cao Jie and Wan Jianru
With the continuous increase in the number of tall buildings and the rapid development of intelligent buildings, more and more demands have been made on the elevators in such buildings. In order to improve their transportation capacity and service quality, a new elevator control method in elevator group control has been rapidly developed. The elevator group control system consists of three or more elevators run as a group for system management.[3] At the same time, the elevator group control system can also reduce the power loss in the elevator running process.
The group control algorithm mainly considers the following three control objectives: low latency, low longtime waiting percentage and low power loss. With the rapid development of computer technology and the theory of artificial intelligence, it has been widely used in the field of elevator group control.
Currently, many experts put forward many intelligent control algorithms, such as scheduling method based on fuzzy control, expert system, neural network and genetic algorithm. In addition, the passenger flow of elevators is different in various floors, and the trend of passenger flow is different in different time intervals. So, a method is put forward by analyzing the building, the situations of elevators and passenger traffic flow through computer technology to seek the optimal scheduling strategy for elevator control.
Compared with traditional elevator scheduling, these studies have significantly improved the elevator performance and greatly developed the elevator group control method. However, analysis of them has uncovered the following shortcomings:
- The setting of control index for all floors is the same, not considering the natural characteristics of floor property.
- Traffic pattern set is basically fixed, which cannot dynamically reflect the change of passenger flow.
- Congestion in the elevator car is not considered.
The concept of “floor property” is put forward based on analysis of the different points of traffic on each floor. It is used to coordinate the demand for elevators of each floor. Different traffic patterns are reflected in the priority, and are considered objectively. The traffic-flow expansion method is used to convert traffic patterns. The congestion status of passengers in an elevator car and degree of human comfort are often considered.
Floor Property
With rapid economic development, more and more high-rise buildings are being built. Due to this trend, passengers are in elevators longer, which can increase their levels of anxiety. These levels differ when occupants are on different floors, and as the process is repeated (sometimes several times in one day), they can suffer repeated distress. Floor property solves this problem to reduce the riding time of passengers on high floors and provide them better elevator service.
Floor property involves setting a constant greater than 1 or equal to 1 to different floors to characterize its properties and selecting a layer as a floor boundary through the comprehensive analysis of building height and passenger flow. This makes the floor properties below the boundary to be 1, with the floor properties above the boundary according to the principle of increment. In order to facilitate programming, arithmetic progression is utilized to attribute a floor-property value to each floor. We can use this to calculate passenger waiting and riding times by using a weighting method, getting a comprehensive riding time:
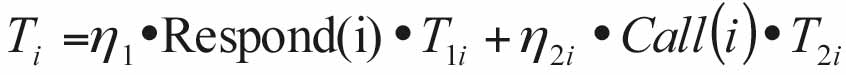
where i is the floor number where passengers are, T1i is the riding time of the passengers in the elevator car, and T2i is the waiting time. The accurate values of T1 and T2 can be obtained by the internal call signal and the calls assigned to the elevator. Respond(i) and Call(i) are the priorities of calling and responding, respectively.
η1 is the psychological factor of the car, which reflects the mental calm degree of the passengers in the elevator car. The value is ratio of “people-feel” to “practical” time. Most people feel time passes more slowly in an elevator car and hope to be able to arrive at their destinations as soon as possible. For example, having been in an elevator car for 30 s. may feel like more than 40 s. In this situation, the psychological factor of the car is 40/30 = 1.33. In general, this is a number greater than 1. For the purposes of evaluation in this article, the value is set as 1.1. η2i is the floor property of the ith floor.
Priority Analysis
According to differences in traffic, building elevator group control traffic modes are divided as follows:
- Up-peak model: most traffic flow is upward, and most passengers wait at the first floor, so the elevator should respond to a first-floor call as soon as possible. This necessitates improvement of the first floor’s priority of calling.
- Down-peak model: most traffic flow is downward. Most passengers are looking to reach the first floor, so the elevator should improve the first floor’s priority of responding.
- Random model: the numbers of passengers going up and down are basically the same, as is traffic demand between the different layers.
- Two-way model: the main passenger flow is going toward or coming from a floor that is not on the first level: for example, a restaurant during lunchtime.
Through the above analysis, it can be found that each floor’s priority of calling and responding needs to be modified as passenger flow changes. In order to guarantee efficient elevator operation and achieve optimal elevator dispatching control, the value of each floor’s priority of calling can be obtained by the total number of people in the elevator car (placed by the weight w1i) in a fixed time, Tfix. Similarly, the value of the level’s priority of responding can be obtained by the total number of people in the elevator car (placed by the weight w2i) in Tfix.
The value of Tfix relates to the number of floors and elevators, and the characteristics of the traffic-flow changes, set as 5 min. for the purposes of this research. Because passenger flow in up- and down-peak models change rapidly, the corresponding priority should have the characteristics of rapid change to meet the rapidly changing passenger flow. Change of passenger flow is represented by the change of weight in the elevator car. Call(i) represents the priority of calling, and Respond(i) represents the priority of responding. These values are defined as follows:

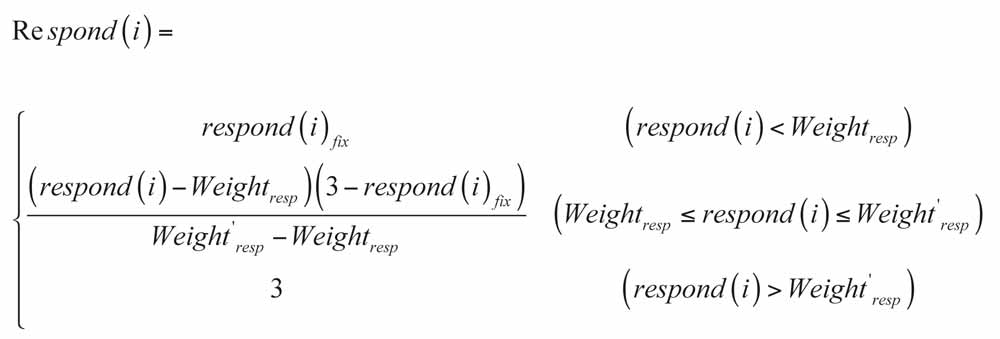

Δw1i and Δw2i represent the total weight that enters and leaves the elevator car, respectively. λ is the coefficient of passenger flow. λe is the enlargement multiple of passenger flow, which is used to reflect the probability of the occurrence of large passenger flow (set as 3 in this article).
From Equations 1 and 2, we can find that call(i) and respond(i) change as elevator traffic changes. In order to ensure call(i) and respond(i) are not zero when the elevator does not work, in Tfix, when call(i) and respond(i) are less than weightcall and weightresp, make the call(i) and respond(i) equal to call(i)fix and respond(i)fix. At the same time, to limit the permissions of call(i) and respond(i), when their values are more than weight’call and weight’resp, make call(i) and respond(i) equal to 3.
According to Equation 1, the value of Ti is related to the value of call(i) and respond(i). The elevator can respond to the hails from the floor that has greater values for call(i) and respond(i) more quickly, thus enabling it to move to that floor more quickly.
Function of Congestion Degree Evaluation
An excessive number of people in the elevator car will make passengers feel crowded, reducing the comfort factor. This article takes reducing the degree of congestion as a control target of the elevator group control system. Car congestion can be represented by the weight of the elevator car. If the weight in an elevator is relatively large when the car is called, the elevator is considered crowded. So, we can use the function of the weight in an elevator car to represent the comfort factor. In addition, considering the congestion may occur in the riding process, the degree to which the passengers in the elevator are uncomfortable can be represented by the current function of weight in an elevator car and the function of elevator direction, which is a nonlinear increase function to weight. When the weight is small, the function value changes a little; when the weight is close to the limit of the elevator car, the value changes rapidly. So, the function of degree of discomfort can be expressed as:
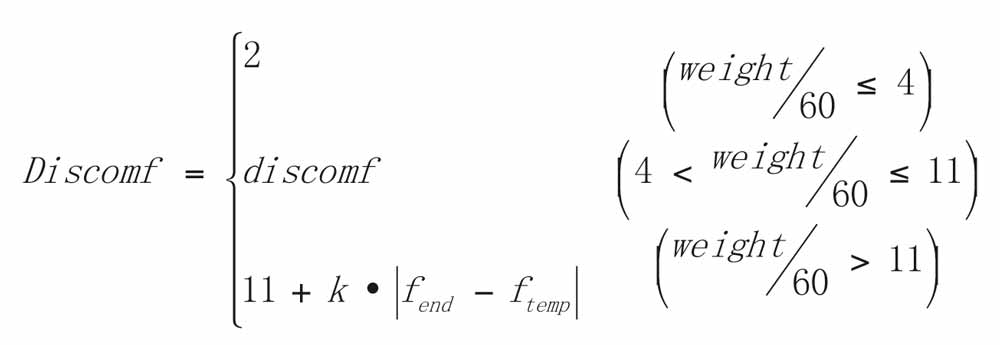
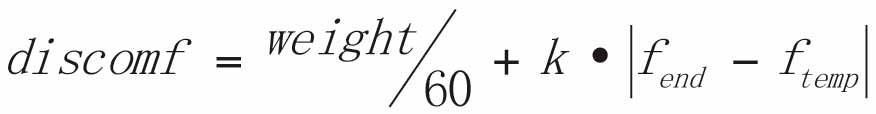
where fend is the farthest floor (the highest layer when the elevator going upward and the lowest layer when the elevator going downward); ftemp is the floor from which the calling signal originates; weight is the weight in the elevator car; and k is the congestion coefficient of prediction, decided by the floor number and passenger-flow density (ranging from 0.1 to 0.3[2]), which is 0.2 in this example.
For the elevator, I, the function of congestion degree evaluation that responds to all assigned elevator calls can be expressed as:
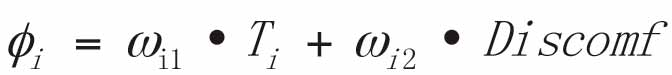
wi1 and wi2 are the coefficient of time weight and the congestion degree coefficient, respectively. So, the function of the congestion degree evaluation for the current elevator-sending scheme is:
wi1 + wi2 = 1 (Equation 8)
After various targets have been identified, how to find the best allocation method becomes key. Because optimization ability of genetic algorithm (GA) is very strong, the paper uses GA to seek the optimal allocation of calling distribution. The following example is of a 30-floor office building with four elevators.
Coded Form
Using the variable gene chain length and coding in binary, four elevators are respectively presented by 00, 01, 10 and 11. For example, 100100110110 represents that the first call is assigned to elevator 10, the second is assigned to elevator 01, and the third is assigned to elevator 00. When a call is placed, the gene chain will have a unit length gene. When there is a new calling signal, it makes the gene chain length add 1, and while the signal is assigned to an elevator, the gene chain length will reduce 1. The chromosome length is the current elevator number waiting for distribution. Define the array x(i) (i = 1, 2… 2n – 2), where n is number of the floor, and each array element represents the uplink calling signal of 1 to the n – 1 floor and the downlink calling signal of n to the second floor. The latter value is 1 when it has calling signal; otherwise, it is 0. A variable-length gene chain length is 1 in the array elements, according to which floor the call is connected with the gene.
When there is a new call, a time calculation of seeking the optimal allocation will be made. This allocation will be imported into Bestgene. The initial value is 0 without calling signal. Only one calling signal is given to the elevator at any one time. When the elevator car arrives at the floor from which the calling signal came, a recent calling signal is selected from the gene chain and assigned to the elevator, making the value of the elements array arranged, which represent the floor to be 0 at the same time.
Each elevator will take calls assigned from Bestgene into its queue. If Bestgene only assigned a calling signal, it will be made a number in the elevator’s taskbar. If more than one signal is given, the signal running in the same direction as the elevator will be placed atop the most recent call number in the taskbar. Set the value of the array x(i) that corresponded to the calling signal in the taskbar to 0. Each elevator’s taskbar call and internal choice decide the elevator’s operation scheme (Figure 1).
Figure 1: The process of assigned calling in the dynamic gene chain
Generation of Initial Population
If established expertly, the initial group produces good individuals that can speed up the search. Thus, part of the initial population is generated based on expert rules, and another part is produced randomly.
Design of Fitness Function
Genetic algorithms judge advantages and disadvantages based on the value of fitness function in each ladder scheme. Greater fitness values of individuals have more chances to reproduce the next generation. In practical application, the fitness function needs to be designed according to itself. The fitness function is expressed as:
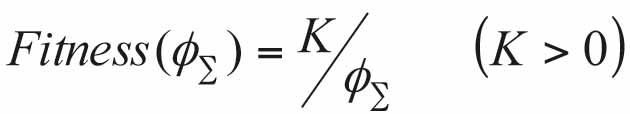
Selection
In order to guarantee the stability of the dispatching algorithm, use the selection operator, which combines the fitness proportional method and the best combination of individual methods. The dispatching scheme that uses a genetic algorithm optimized of the best individual preservation method will not be less than the best individual in the initial population, which ensures stability of the dispatch algorithm.
Crossover and Mutation
Use the two-point crossover operator in genetic operation. Use the two mutation operations according to specific conditions:
Site mutation operator, used for the individuals in the population whose fitness is less than the average.
Mutation of two-point interchange, carried out upon the individuals whose fitness is greater than the average. The mutation rate should not be made too small to avoid getting into a local optimal allocation in the process of seeking the optimal solution.
When the calling is less, take the way of traversal to search optimization if the calculation of capacity can keep up. This article selects 4 as a cutoff point. When the call number is not greater than 4, take the way of traversal search optimization. When the call number is greater than 4, use genetic algorithm (Figure 2). T is the maximum genetic algorithm value.
Analysis of Experimental Results
The simulation is run on the group control system with 30 floors and four elevators, in which the elevator rated speed is 2 mps. The restaurant is located on level five. Usually, in such a model, traffic is simulated randomly in a certain range, and there is mutual restraint. The starting and terminal floor is decided by the Monte Carlo method: at noon, assume 35% of people on each floor go to the restaurant, 40% go out, 15% do not change floors, and 10% randomly go to other floors. Passenger traffic is distributed in accordance with time according to a Poisson distribution.
call(1)fix = respond(1)fix = 2 (Equation 10)
call(5)fix = respond(5)fix = 1.5 (Equation 11)
call(i)fix = respond(i)fix = 1 (i ≠ 1, 5) (Equation 12)
Weightresp = Weightcall = 300 kg (Equation 13)
Weight’resp = Weight’call = 1200 kg (Equation 14)
The property of each floor is:

| Layer | Average Waiting Time | Long Time Waiting Rate | Average Lunch Waiting Time |
| 5th | 32.1 s. | 10% | 23.3 s. |
| 25th | 27.6 s. | 7% | 29.5 s. |
| Average | 29.4 s. | 9% | ———— |
Table 1: Simulation results
This method reduces the transport cost difference of each floor. The elevator efficiency of each floor is relatively high; along with the change of traffic demand and change, the elevator can be dispatched in a timely manner.
Summary
The floor-property concept has been put forward. Comprehensive consideration for various floors has been taken to avoid obvious differences between different floors so passengers in high rises do not feel they wait longer for elevators than passengers in low rises. The simulation program is programmed in Visual Basic. Its flowchart appears in Figure 3.
Figure 3: Simulation program flowchart
For the transportation mode, the priority of calling and priority responding (instead of a fixed pattern) has been proposed. In the mode of priority of calling and responding, the priority of each floor could be automatically changed with the change of passenger flow. For the up- and down-peak condition, the priority in the special period can be quickly changed to adapt to the sudden changes in traffic patterns. In the method of optimal scheduling choice, the piecewise way is considered. When there are fewer assigned calls, the traditional way is selected. When there are more assigned calls, the GA is used. The variation of flow is considered in this design; therefore, it is suitable for various types of buildings, and it only needs to modify a fixed value, according to the actual situation for different buildings.
Acknowledgements
This research was supported by AQSIQ Nonprofit Industry Specialized Research Funding (No. 2012104016 and 201310153).
References
[1] D.E. Goldberg. Genetic Algerithms in Search, Optimization, and Machine Learning. New York:Addison Wesley, 1989.
[2] Zengchang Li. “Research on Intelligent Control Strategy for Elevator Group.”Tianjin University, 2004.
[3] Chang Bum Kim, Young A. Seong, Hyung Lee-Kwang. “A Fuzzy Approach to Elevator Group Control System.” System and Cybernetics. 1995,(5): 985-990.
[4] Yu Cai, Wan. “Elevator Control Based on Fuzzy—Logic and Neural Network.” China Elevator. 1999.010(002): 34-38.
[5] Rangen Fang. Computer Simulation and Monte Carlo Method. Beijing: Beijing Institute of Technology press, 1988.
[6] Xiaoping Wang, Liming Cao. Genetic Algorithm: Theory, Application and Software Implementation. Xi’an:Xi’an Jiao Tong University Press, 2002.
Get more of Elevator World. Sign up for our free e-newsletter.









