Elevator Group Control Optimal

Scheduling Policy

by Zheng Jiong, Bu Siqing and Wan Jianru

Elevator systems’ service quality and service efficiency play extremely important roles in the effective use of high-rise buildings. More and more buildings have installed multiple elevators to meet the increasingly heavier task of transporting passengers. To improve the service quality and service efficiency of the elevator, elevator-control technology has developed from a single independent control to coordinated control of multiple elevators, which is the elevator group control. Developed in recent years, fuzzy and neural-network control methods have overcome the uneven and “cluster” problem of busy elevators caused by the traditional partition method and can improve the efficiency of the elevator to a great degree.

However, the weighting coefficients of the membership function in the fuzzy control method is hard to change, difficult for self learning and determined by different traffic patterns. The neural-network control method needs a longer initial learning time due to its bad early-learning ability, and it is sometimes difficult to ensure convergence to the global optimum.

GA is a new discipline based on Charles Darwin’s theory of evolution and a computer simulation of it. It is a global optimization search algorithm that searches for the best solution according to survival of the fittest. In this article, the short average waiting time, the short riding time, low crowding and little energy consumption are regarded as the main targets of elevator group scheduling. GA is used to realize the optimal scheduling of the elevator group. Dynamic simulation running results demonstrate the feasibility and advantages of this approach, compared with the aforementioned commonly used methods. The main performance indicators (such as waiting time and riding time) are shortened.

Establishment of Performance-Evaluation Functions

For multiple-elevator group control, the main indicators of performance evaluation are the average waiting time, average riding time, long waiting rate, elevator crowding, energy consumption, etc. The most concern is about how to shorten the waiting time and achieve fast and stable rides to the destination. According to the people-oriented principle, the shorter average waiting and riding times, less crowding and less energy consumption are the main control indices of elevator scheduling. Define the evaluation function of the ith lift responding to the jth landing call signal as in Equation 1, and the elevator with the smallest evaluation value responds to the jth landing-call signal.

F(i,j) =W₁F_w(i,j)+W₂f_r(i,j)+W₃f_n(i,j)=W₄f_e(i,j) 1 ≤ i ≤ M                                               (Equation 1)

where f_w(i,j) is the estimated passenger waiting-time cost function when the ith elevator responds to the jth landing call signal. f_r(i,j) is the estimated passenger riding-time cost function when the ith elevator responds to the jth landing call signal. f_n(i,j) is the valuation function of the estimated number of passengers inside the car when the ith elevator responds to the jth landing call signal: the greater the value, the fewer the passengers. f_e(i,j) is the estimated energy-consumption cost function when the ith elevator responds to the jth landing-call signal. M is the number of elevators participating in the group-control operation. W₁, W₂, W₃ and W₄ are importance weighting coefficients, which satisfy W₁ + W₂ + W₃ + W₄ = 1.

Waiting-time function f_w(i,j) and riding-time function f_r(i,j) can be estimated by considering speed, opening and closing times, the number of passengers in and out of the car, the command-signal status in the car and the allocated landing-call signal state. The motor is in a state of renewable power generation when the elevator is up with empty load or down with full load, and the regenerated energy can be fed back to the grid. The group-control system can preferentially allocate such an elevator in the running state for the landing-call signal to save energy. The elevator in the starting, acceleration and deceleration stage consumes more energy, so the elevator should try to run less to carry more passengers. This would make it stop a minimal number of times to reduce energy consumption. By changing the weight coefficients of W₁, W₂, W₃, etc., the elevator can be adapted to different models of elevator traffic flow. When it is in the upward and downward traffic peak, waiting and riding times are prioritized, and their importance factors of W₁ and W₂ will be increased.

Optimization Design of GA

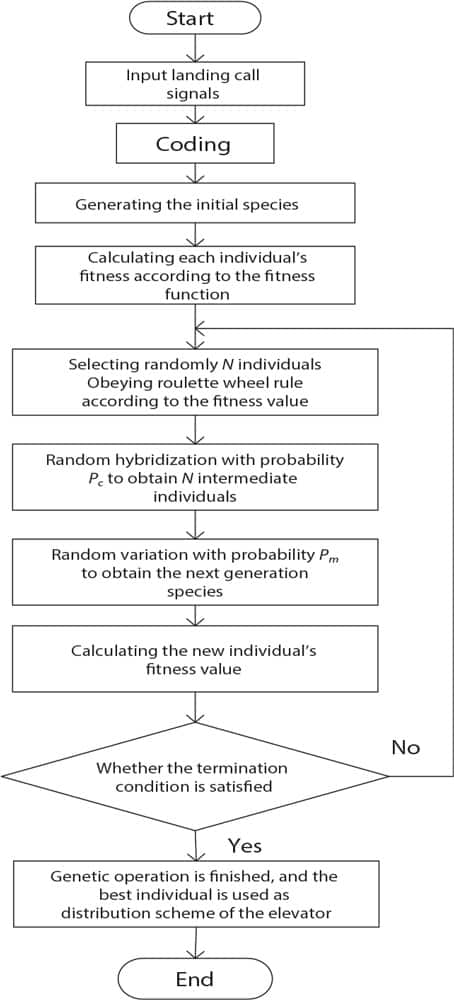
The traditional scheduling algorithm always distributes an elevator to respond to a landing-call signal. Once a landing-call signal is assigned to an elevator, this distribution relationship is determined. After the new landing-call signal is generated, the previous call-signal distribution is treated as a known condition and will not be changed.

However, the new landing-call and command signals in the car continue to be generated; therefore, the original optimal conditions may be destroyed. As the number of in and out passengers is random and the car door is open for a long time, predictions of the opening and closing times and the actual time after the elevator stops may be different. Therefore, the original distribution relationship needs to be corrected according to the new conditions. GA is a kind of efficient parallel global search method for solving problems and can modify the original distribution relations according to the new state of the elevator. In the case of multiple landing-call signals, GA can search for the optimal scheme of elevator distribution.

Coding

Before the GA is in search, the problem to be solved is expressed as a “chromosome.” The chromosome in this design uses integer coding, which can directly represent the assignment of landing-call signals, while simultaneously simplifying the coding and decoding process. The chromosome length is the number of currently not-responded-to landing-call signals, which uses a variable length chromosome, the length changing with the number of the landing-call signals. It has two advantages: first, it does not have to take a longer chromosome, reducing the amount of computation. Second, it does not produce valid solutions.

In each optimization, if there are L unacknowledged landing-call signals, the “chromosome” is represented by an integer code string with the length, L. For example, each number of 132142 represents a service-elevator number of a landing-call signal. Different code strings represent different allocation schemes. At the same time, an array, callnote (28), is used to record the number of assigned landing-call signals. To four 15-story elevators, for example, layer 1-14 upward call signals are recorded from 1-14, and layer 2-15 downward call signals are recorded from layers 15-28. Corresponding to a chromosome with code 132142, if the values of callnote (0) to callnote (5), respectively, are 1, 7, 12, 16, 18 and 26, layer 1 downward and layer 3 upward landing-call signals are assigned to elevator 1. A layer 7 upward landing-call signal is assigned to elevator 3. Layer 12 upward and layer 13 downward landing-call signals are assigned to elevator 3. A layer 5 downward landing-call signal is assigned to elevator 4.

Generating the Initial Chromosome Group

To increase the search speed of the GA, some better individuals are first produced and added to the initial chromosome group according to expert experience. Second, a number of chromosomes are generated randomly and added into the initial chromosome group. Finally, the initial chromosome group is generated. Each chromosome is called an individual, while N individuals constitute a species. The GA uses the species as an initial point for iteration.

Design of Fitness Function

The fitness function indicates the individual’s ability to adapt to the environment. GA in the evolutionary search depends on the fitness-function value to determine the stand or fall of each individual, and individuals with larger fitness values will have more opportunities to breed the next generation. In a species, the total fitness function of the kth individual with L unacknowledged landing-call signals can be expressed as:

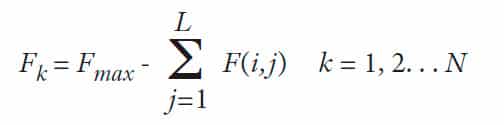
where F(i,j) is the evaluation function value when the jth landing call signal is assigned to the ith elevator in the jth individual, which can be calculated by Equation 1. Fmax is a large constant value for the purpose of minimization. The evaluation function is converted to the maximization of the fitness function in order to meet the requirements of the GA. Fk represents the performance of the distribution scheme represented by the kth individual in the species. The larger Fk is, the better the allocation scheme.

Selection

A roulette-wheel selection mechanism is used to perform selection operation. The ratio of individual fitness value to the sum of all individual fitness values is used to represent the probability the individual is selected:

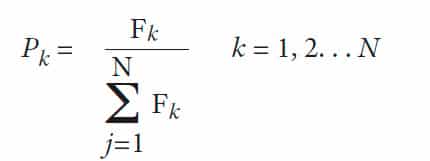
Meanwhile, the optimal individual preservation strategy is used, in which individuals with the highest fitness values are directly copied to the next generation without cross-pairing. Therefore, optimal individuals in each generation can be preserved.

Chiasma

Chiasma is performed in two steps: first, the two code strings to be matched are randomly taken from the species. Second, the information in these two code strings is exchanged to generate a new code string. Single-point random hybridization is used. One pair of parent individuals is divided into two parts from the intersection point, which randomly determines a gene as the intersection point with equal probability. Two new individuals are obtained by exchanging the latter part of two individuals with probability Pc. Two new individuals contain the characteristics of their parents, making it possible to combine the best features of their parents to get a better individual.

Variation

Within the species, an individual is randomly selected, and a bit of the string code is changed with a certain probability. The randomly generated number from 1 to 4 (there are four elevators) is used to replace the original number. Variation probability controlled by Pm is generally from 0.001 to 0.01. The main role of variation is adding new feature genes to the species, so the GA has the ability to escape from local optima, while also providing opportunities for the generation of a new distribution scheme.

Calculation of the New Individual Fitness Value

Determine whether the termination condition is satisfied. If so, go to the following section “End of Genetic Algorithm Operation.” Otherwise, return to the “Selection” section to continue iteration.

End of GA Operation

The optimal individual obtained in the entire operation of the GA is used as the elevator distribution scheme, then such allocation scheme is output to the controller of the elevator car. Thus, one optimization process is finished.

Running of Dynamic Simulation

According to the above method of GA optimization, VB programming is used to implement elevator optimal scheduling algorithm. To verify the feasibility of the GA to achieve the optimal scheduling (with four 15-story elevators as the control object), a Visual Basic-based elevator simulation system is used. Based on the above scheduling policy, the simulation includes the system parameter setting module, initial state setting module, simulation run module, simulation run results module, etc.

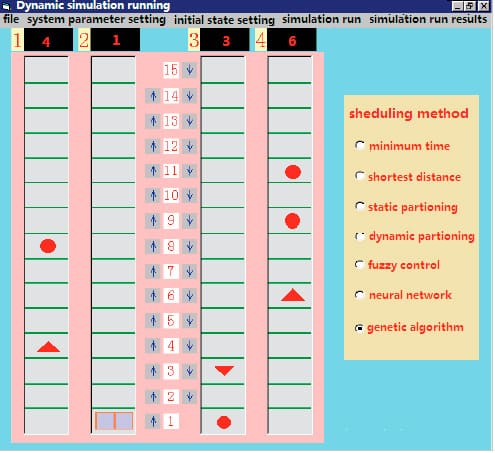
Figure 2 shows the dynamic simulation run interface. This is the main interface of simulation software, which is first displayed when the software is running. Before the simulation is carried out, in the menu bar, click on the system-parameter setting and initial-state setting.

Figure 3 is the system-parameter setting interface. The various parameters (including those of the building, elevator and elevator traffic conditions) should be input. Figure 4 is the initial-state setting interface. This includes current floor and running state, registered internal selection signals and each elevator’s allocated external call signals. There are seven kinds of running states:

• Parking
• Upward(ACC), which indicates the elevator is accelerating, running upward
• Upward(DEC), which represents the elevator is decelerating, running upward
• Upward(stop), which represents the elevator is parked at the current floor and waiting for passengers to enter and exit, after which the elevator will continue to run upward.
• Downward(ACC)
• Downward(DEC)
• Down(stop)

The user can choose a running state from the dropdown list. When all parameters have been set, a scheduling algorithm can be selected at the right of the simulation running interface panel; then, the dynamic simulation run can be carried out. At the end of it, in the menu bar, click on simulation run results. In the results interface diagram, the indicators that reflect the effect of group control algorithm can be derived. A passenger traffic simulation model from Elevator Traffic Analysis Design and Control is used.[1] The time of passengers reaching the floor obeys the Poisson distribution, and the start and end floors are determined by the Monte Carlo sample method. Based on the input passenger parameters, the program automatically produces a series of landing-call signals. It also receives these signals in real time, selects the appropriate dispatching program and controls the operation of each elevator. It will keep records of each passenger’s waiting time, riding time, etc. After the simulation process is finished, various performance indicators can be obtained in the simulation-running results interface.

When a new landing call signal is generated, the scheduling algorithm is invoked to determine which elevator should be assigned. When the genetic operation is completed, the optimal distribution scheme according with the best individual can amend the original distribution relationship and overcome defects of the original unreasonable allocation caused by changing conditions. Once an elevator is stopped, the scheduling algorithm is called again to calculate whether the allocation of the elevator assigned to the landing-call signal is reasonable. The unreasonable elevator allocation will be revised by another elevator to respond to the landing-call signal.

Analysis of Dynamic Simulation Run Results

System parameters are set as follows: total number of floors: 15; first floor height: 3.5 m; top floor height: 3.5 m; other floor height: 3.0 m; number of elevators: 4; capacity of the elevator: 17; rated speed: 2.5 mps; acceleration: 1.5 mps2; jerk: 2.0 mps3; opening time: 2.0 s.; closing time: 2.5 s.; arrival rate of passengers: 1 person/s.; upward traffic percentage: 0.9; downward traffic percentage: 0.05; interfloor traffic percentage: 0.05. In this article, the GA optimization scheduling, forward neural network control and fuzzy control methods were carried out in a dynamic simulation program under the same conditions. In the upward peak period, Figure 5 shows the dynamic simulation run results by GA after 80 passengers are serviced. Similarly, the dynamic simulation run results by neural network and fuzzy control can be obtained.

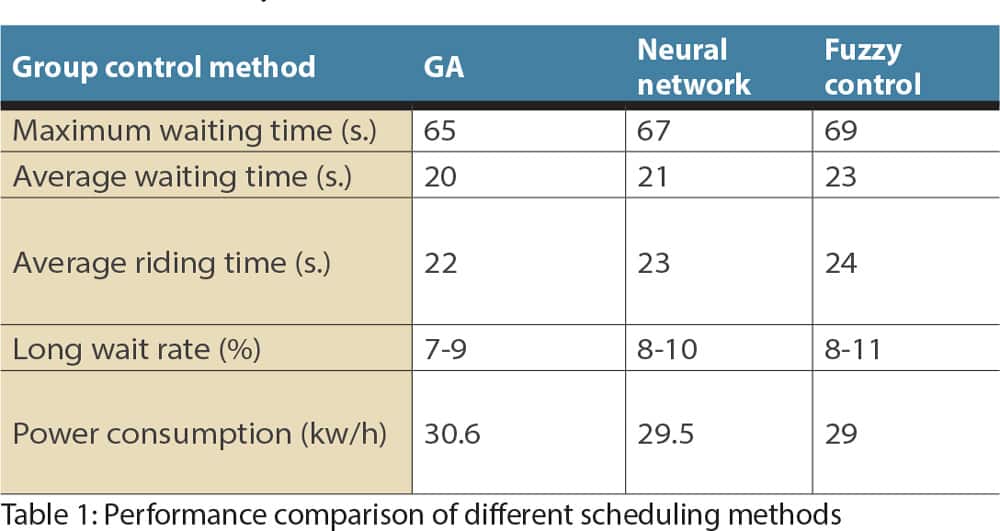
Comparison of the three different scheduling methods’ performance is shown in Table 1. As can be seen from the data, elevator group control key performance indicators of the proposed GA optimization scheduling method, such as the average waiting and riding times and long waiting rate are better than the neural network and fuzzy control methods.

Conclusion

According to the diversification of elevator group control system control objectives, a multi-objective optimization group-control scheduling policy based on GA was proposed. The waiting and riding times, crowding, energy consumption and other control targets were optimized to improve the overall service performance of the elevator group. By using GAs to achieve optimal elevator-group scheduling, four 15-story elevators were used for dynamic simulation. Dynamic simulation results demonstrated the feasibility of this method. The main performance indicators significantly improved, compared with the static and dynamic partitioning methods, and the commonly used methods of fuzzy and neural network control.

Acknowledgement

Special research projects funded by AQSIQ Public Welfare Industry (2012104016, 201310153).

References
[1] Barney, G.C.; Dos Santos, S.M. Elevator Traffic Analysis Design and Control[M]. England: Peter Peregrinus 1985.
[2] Jianru, Wan; Yu, Cai; Yinhui, Li. “Elevator Group Control Policy Based on Fuzzy and Neural Network Control”[J]. Electric Automation, 1999, 4: 21-24.
[3] Jianru, Wan; Chunjiang, Liu; Hongchi, Liu. “Elevator Group Control Policy Based on Forward Neural Network Control”[J]. Hoisting and Conveying Machinery, 2002, 6: 23-27.
[4] Jianru, Wan; Zhichao, Zhang; Yingpei, Liu. “A New Elevator-Group Control Method Based on the Blending of GA and Neural Network”[J]. ELEVATOR WORLD, September 2007.
[5] Hong, Shen; Jianru, Wan; Zhichao, Zhang. Elevator Group-Control Policy Based on Neural Network Optimized by GA[J]. Trans. Tianjin Univ. 2009, 1 5: 245-