Escalator Fractal Behavior, Part Three

The fractal dimension values of two escalators are compared in this penultimate entry in the series.

by Dr. Ali Albadri

This installment will compare the fractal dimension (Df) values of two escalators: one free of any mechanical defect and another with a mechanical defect. Like our previous comparison study (with and without passenger),[1] this article will show whether the mechanical failure can be detected using the technique of estimating the Df values. Quantifying escalator behavior when it has a defect or it is free of one can offer a big advantage for escalator maintainers. It will help them define quantitative level indicators to distinguish between escalators with and without problems. They will help define a system for prioritizing maintenance schedules to the escalators’ needs. The principles of the methodology used in this study can be implemented in any other mechanical or electrical products.

Introduction

Escalators are complicated and accurate. They consist of individual components and subassemblies that interact with each other to produce physical motion in the step band, which is used to transport passengers from one level in a building to another.

It is vital for assets-management companies to keep escalators in good and sound operation. Therefore, they try their best to adopt and deploy well-thought-out maintenance plans by which to reduce the financial impact of escalators being out of service. Additionally, passenger frustration can build up when users must walk the 17-20-m rise of a unit if it is out of service.

A variety of monitoring devices has been used to monitor individual escalator components or subassemblies. To see the signals from these devices, one need go no further than the escalator control panel. These monitoring systems can detect trends before and after a mechanical failure, helping the maintenance company know which steps to take to restore failure trends to failure-free ones. This is especially helpful before the machine goes out of service. However, monitoring systems have proven expensive and usually have high maintenance costs themselves. Their proper use needs trained people who can make educated predications to identify mechanical failures.

The resilience of the mechanical interactions between the mechanical components and subassemblies inside an escalator depends on the criticality of their mechanical interaction. Like any complicated network, these critical components/subassemblies can act like nodes. Failures in critical individual nodes can cause catastrophic failure in the whole mechanical system, causing the escalator to be taken out of service. The tipping point develops when small events cause minor problems in the critical nodes. These minor issues balloon over time to major disruptions because they are difficult to detect by either the maintenance team or the escalator self-monitoring system.

An invention like the smart step[2 & 3] can solve all the problems mentioned above at once. The natural operation of the smart step is that it scans many of these critical nodes within a few cycles of escalator operation. We have come up with a technique derived from the chaos and complex systems theory to process the data from the smart step.[1 & 4] It deals with translating the data as if they are generated from a nonlinear system. The interactions between the components and subassemblies make them behave in a nonlinear way. Our technique uses Df as a quantitative value to characterize the operational performance of an escalator. We presented the potential of an interesting relationship between Df and the stress level in an escalator step band.[4] The values of Df are used to show the effect of passenger loading on measured data from the smart step. It showed that passengers created more peaks and troughs in the spectrum of the measurements, causing the
values of Df to increase. In another study, we divided the overall complex spectrum into individual regions inside the escalator.

This proved that the overall Df for an escalator is the mathematical sum of the Df values of the individual regions.[5]

Methodology Used to Determine Df

Like our previous studies,[1 & 4] Df was determined using the scaling step technique. The technique has also been used by other authors in various applications.[6-11]

The smart step in this study has two strain gauges, mounted at critical components on the step. The criticality and sensitivity of the components in the step to the mechanical loadings and to the generated stress levels in the step was assessed by conducting various finite element analysis simulation loading scenarios onto it.

The smart step was run for short periods of time in two escalators, A and B. Figures 1-4 show the traces for the data obtained from the two strain gauges after running the smart step in escalator A, then B. The runs were done when the escalators were free of passenger loading. Figures 9-12 show the estimated Df values for the complete traces of strain gauges 1 and 2. The estimated values are tabulated in Table 1.

Results and Discussion

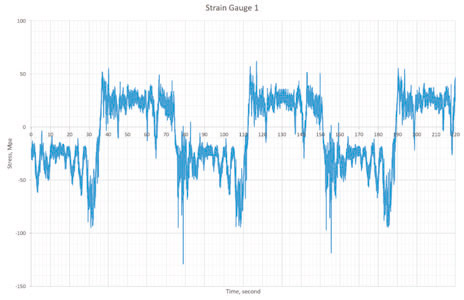
Although the nature of the traces in Figures 5 and 7 might look rougher than the traces in Figures 1 and 3, the relative variations in the spectrums of Figures 1 and 3 are much higher than those in Figures 5 and 7. In fact, the traces in Figures 5 and 7 are typical of an escalator free of any mechanical defect. However, Figures 1 and 3 show that escalator A has a problem, which becomes obvious when the figures are studied in detail (Figures 2 and 4). Comparing Figures 2 and 4 suggests the smart step was subjected to a higher stress level at strain gauge 1, when compared to strain gauge 2, especially on the return side. The stress level exceeds 100 MPa at strain gauge 1, compared to 15 MPa at strain gauge 2. The measured stress levels in escalator B did not exceed 10-12 MPa in the measurements from both strain gauges.

Visual examination was conducted on both escalators to determine the reason for the differences in the data. It was found that the loading-relieving ramps on the return side of escalator A were completely out of alignment.

The consequences of these findings are high stress levels recorded by strain gauge 1 and high roughness in the traces of escalator A, compared to those from escalator B. This behavior has been quantified using the values of the fractal dimension concept. The Df values from running the smart step in escalator A are higher than the Df values of the traces, which have been obtained from running the smart step in escalator B. Table 1 shows how both gauges 1 and 2 produced exactly the same Df for escalator B.

Conclusions

This study has proven that Df can be used to quantify behaviors of escalators, regardless of whether they have mechanical defects. The escalator with a mechanical defect produces rougher traces of measurements, with higher Df values compared to those of the escalator free of any defect. Df increases by about 3.6%. It is also interesting to note that the estimated Df for both strain gauges are the same, 1.569, for escalator B, which is free of any mechanical defect. This implies that the Df values are independent of the location of the strain gauges in the step when the smart step is run in an escalator free of any mechanical defect.

References
[1] A. Albadri. “Escalator Fractal Behavior, Part Two,” ELEVATOR WORLD, December 2020.
[2] A. Albadri. “Tube Lines Gets Smart to Monitor Escalator Wear,” Computer Weekly (07/01/2008).
[3] A. Albadri. “Smart Step Measures Escalators’ Heartbeats,” EW, September 2020.[4] A. Albadri. “Escalator Fractal Behavior, Part One,” EW, October 2020.
[5] Francis C. Moon, “Dynamics and Chaos in Manufacturing Processes,”
Wiley Series in Nonlinear Science, 1998.
[6] Athanasia Zlatintsi, “Multiscale Fractal Analysis of Musical Instrument Signals With Application to Recognition,” Institute of Electrical and Electronics Engineers (IEEE) Transactions of Audio Speech and Language Processing Vol. 21, No. 4, April 2013.
[7] J.D. Victor. “The Fractal Dimension of a Test Signal Impactions for System Identification Procedure,” Biological Cybernetics 57, p. 421-426 (1987).
[8] Chang-Ting Shi. “Signal Pattern Recognition Based on Fractal Features and Machine Learning,” Applied Sciences 8, p. 1,327 (2018).
[9] Dumitru Scheianu and Ion Tutanescu, University of Pitesti,
Electronics, Communications and Computers Department.
[10] P. Marago and A. Potamianos. “Fractal Dimensions of Speech Sounds: Computation and Application to Automatic Speech Recognition,” Journal of Acoustical Society of America No. 195 (3), March 1999.
[11] R.H. Riedi, M.S. Crouse, V.J. Ribeiro and R.G. Baraniuk, “A Multifractal Wave model with application to Network Traffic,” IEEE Transactions on Information Theory Vol. 45, No. 3, April 1999.