The Maximum Speed of Elevators
May 1, 2016

Furthering ideas on “How Fast Could the Fastest Elevators Be?”
Elevators traveling over long vertical distances at high speeds must be considered impossible. This advantage has been reserved by the laws of nature for horizontal travel. Having read with interest the article “How Fast Could the Fastest Elevators Be?” by Dr. Albert So and Ricky Chan (ELEVATOR WORLD, February 2016), I am glad the writers accept the challenge from EW in the Comment “Further Evaluation of ‘Fastest Elevator’” (EW, December 2014) to join the maximum speed discussion, because architects and building owners need this information to facilitate the planning of express elevators to sky lobbies.
Although all the involved authors have the same concerns — passenger comfort and shortest possible travel times — their views about solutions are different. The article suggests the maximum possible speed of elevators is a complex and difficult problem, though I feel it is a logical task. Your author assumes the maximum tolerable up speed for our hearing organs is 12.5 mps and 8 mps for down trips. These maxima should be investigated by elevator companies and/or medical experts, because they define the maximum speed of elevator cars, as the following will prove and demonstrate. Airtight cars that can control their interior air pressure enable modest time savings.
Maximum Speed of Express Elevators to Sky Lobbies
Figure 1 shows the speed and travel distance for the up trip of an express elevator to a sky lobby at 1,000 m. A distance of 1,000 m enables a car to accelerate to a maximum speed of approximately 31 mps, assuming acceleration and deceleration rates of 1 mps2. The periods for acceleration and deceleration are 32 s. each. For a fraction of a second, the car will travel at its maximum speed. The average car speed will be approximately 1000/64 = 15.6 mps.
The floor level of the car during the up trip is defined by the orange distance line, which also indicates the hoistway air pressure at all levels. For an airtight car, the straight line between 0 and 1,000 m indicates the ideal car internal air pressure for systems to control car air pressure as if the car is moving at an average speed of 15.6 mps. It is obvious that during the first half of the up trip, the car must be depressurized, and during the second half of the trip, the car must be pressurized to give passengers the feeling that the car is traveling at a constant speed of 15.6 mps. Once the elevator arrives at 1,000 m, the doors can open, because during the up trip, passengers have adjusted to the lower air pressure.
In the case of the maximum tolerable up speed being 12.5 mps, the maximum speed of 31 mps must be reduced to 16 mps to realize the shortest possible travel time to the sky lobby, which is defined by 1000/12.5 = 80 s. This up trip is demonstrated by Figure 2.
Figure 3 is valid for a trip of a non-airtight car to 1,000 m and a contract speed of 12.5 mps. For this up trip, the periods for acceleration and deceleration are 13.5 s. each, plus 67 s. at 12.5 mps. The total car flight time is 94 s. The time saving of 14 s. facilitated by an airtight car is lost.
Next, we will consider a sky lobby at 500 m. Over this distance, an airtight car can achieve a maximum speed of almost 22 mps. The periods for acceleration and deceleration will be 23 s. each, and the total car flight time will be 46 s. The average car speed will be 500/46 = 10.9 mps. To achieve the car flight time of 46 s., the car must be airtight, because its travel speed will be higher than 12.5 mps during approximately 20 s.
Figure 5 shows the car flight time for a non-airtight car to level 500 m. In this case, the periods for acceleration and deceleration are 13.5 s. each, and the period at contract speed is 27 s. The total car flight time is 54 s., i.e. 8 s. longer in comparison with the airtight and pressure-controlled option. The average car speed is 500/54 = 9.3 mps.
Pressure-Controlled Cars
Controlling the internal air pressure of airtight cars is a complex technical problem, particularly if we consider the ventilation and air-conditioning needs of cars. To make car doors airtight is a problem all by itself. In case an airtight car is stopped on account of, for example, a power failure, an immediate solution for adequate ventilation will be required to prevent suffocation of passengers. Passengers of airtight cars are possibly exposed to new risks for modest time savings. High maximum speeds entail extra costs for drive systems, safety components, airtight cars and energy consumption.
Concluding Remarks
High travel speeds for long vertical travel distances are probably impossible. So and Chan’s reference to “a pressure adaptation lobby” seems to indicate the writers have the same doubts.
It should be noted that the speed limitations also apply for the vertical travel speed of self-propelled cars. Travel times for down trips can be evaluated with the same methods. The maximum tolerable down speed is even more important than the maximum up speed.
I doubt the viability of airtight cars. The time savings are modest in relation to costs and risks. For very tall buildings, multi-deck local and express elevators with intelligent destination group controls enable configurations that are extremely efficient and save huge amounts of space.
An efficient building of 1,000-m-plus in height seems possible with today’s elevator technology. For the design of very tall buildings, it is essential to investigate the rates of change of air pressure that can be tolerated by the average passenger. Which deviations can be allowed and for how long? Another interesting question is the maximum travel distance of drive systems with cars and counterweights connected by ropes.

Figure 1: If the air pressure at 0 m is 1,015 mbar, at 1,000 m, it will be approximately 895 mbar. 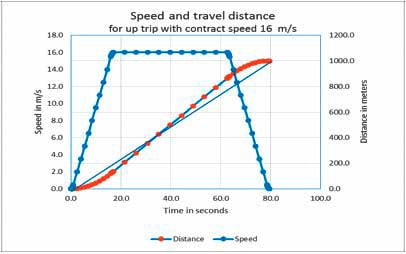
Figure 2: For this up trip, the periods for acceleration and deceleration are 17 s. each, plus 46 s. at 16 mps. The total car flight time is 80 s. The straight line between levels 0 and 1,000 m shows the internal air pressure of the airtight car, which declines as if the car is traveling at 12.5 mps. 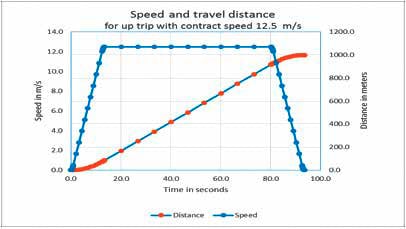
Figure 3 
Figure 4 
Figure 5
Get more of Elevator World. Sign up for our free e-newsletter.