Construction of Poincare Space Map and Phase Plan Map for Escalators, Part 2
Nov 1, 2021

Work repeats that explained in Part 1, but with data derived from passenger loading.
Abstract
In part 1[1], Poincare space map and phase plan map (Poincare section) were constructed from traces of measured data obtained by running the smart step in an unloaded escalator (free of passenger loading). In this study, we are repeating the previous work but for data obtained during passenger loading. Again, and as per our previous study, the constructed maps have confirmed that the data from the smart step have a fractal set nature, even under the influence of passenger loading. The traces/attractors can be described as periodic in closed, semi-elliptical loop shapes that have different sizes as the smart step completes one single run/round in the escalator. The sizes of the loops become bigger with the progression in the run along the coordination of the variables (running time or position of the step in the escalator), then, they turn back to small sizes as they go back to their origin position.
The maps have shown that the measurements from the strain gauges have a damping effect, in the middle and end of the run, in the shapes of small loops. The data in the maps give an indication of a linear relationship in the behaviors of the measured parameters. The constructions of the Poincare space map and the phase plan map (Poincare section) not only confirm that the data has a fractal set behavior, but they also suggest how deterministic or chaotic the variables’ behaviors in the escalator are. Comparing the maps for the data between free-of-passenger loading and with-passenger loading suggests that some loops for some strain gauges are more widespread and open during passenger loading than during the free-loading scenario. This study has confirmed that plotting the Poincare map and the phase plan map can quantitively and qualitatively show the effect of passenger loading on the behavior of the escalator. This could be a powerful tool to be used as a recognizer for machines’ behaviors such as in the development of malfunctions in a machine like an escalator.


Introduction
Poincare map characterizes the interaction of a periodic orbit of a system in the state space of dynamical systems with lower dimensional, and transverse to the flow, subspace called the Poincare section (phase plan map). The dynamics on the Poincare map preserve many of the periodic and quasit-periodic orbits of systems.
Escalators’ behavior can be considered to have nonlinear dynamic patterns. The best example about this behavior is the nature of vibrations inside the escalator. The vibration effect inside the escalator, or any other machine to that effect, can be studied by plotting the Poincare map or phase map for the variables. Nonlinear dynamic mechanical systems have been studied to improve vibration isolation.[2] In recent years, the nonlinear dynamic responses of a rotary bearing system have been analyzed and described in literature.[3] Poincare mapping has also been used to predicate bearing failures.[4]
Previously, and for the first time, we plotted the behavior of an escalator without passenger effect on Poincare map and on phase plan map.[1] The relationship between the space variables was linear and systematic.[1] We showed the progress in developing the close periodic loops for the traces. The maps showed a damping effect within the escalator, as well as the general trend for the behavior of the escalator. In this study, we are repeating the same work but with the effect of passenger loading. The idea is to determine the impact of this variable on the shapes of the periodic loops in the Poincare map and in the phase plan map. This technique shall have significant advantages to machine designers and maintainers. The technique describes what is going on inside the machine — an escalator, in this case — in a graphical way. Consequently, this shall contribute to improving the design of the machines and improve maintenance practices and schedules.
Smart Step Measurements
As per Part 1, the data from smart step were used to conduct this study. The procedure of obtaining the data is similar to what has already been explained in Part 1.
Constructing the Map
In this study, the maps were constructed in a manner similar to that used Part 1. Similar procedure of work and analysis has been used here.
Results and Discussion
Figure 1 shows the phase map for the data of the nine traces (from gauges in the smart step during passenger use). Comparing Figure 1 to Figure 2, which was plotted in our previous study[1], suggests that the loops (attractors) from some strain gauges are wider and bigger in Figure 1 than those in Figure 2. Figure 1 shows traces with dense, repetitive loops that progress to wide open loops as the period of time progresses in the measurements. The data suggest a fractal look with linear relationship between the parameters of the plot. Similar to the study in Part 1, the data have a diagonal layout in the space, confirming the fractal nature of the measurements. Chaos in deterministic systems, like in an escalator or any other similar machine, is sensitive and dependent on initial conditions of the system. This implies that the trajectory of the systems starts close to each other in the phase space, then moves exponentially away from each other for small times. The big and wide loops (attractors) for some strain gauges, in Figure 1, imply that these gauges detected the effect of passenger loading, causing the loops of the attractors to open up and occupy a wider area in the plot.
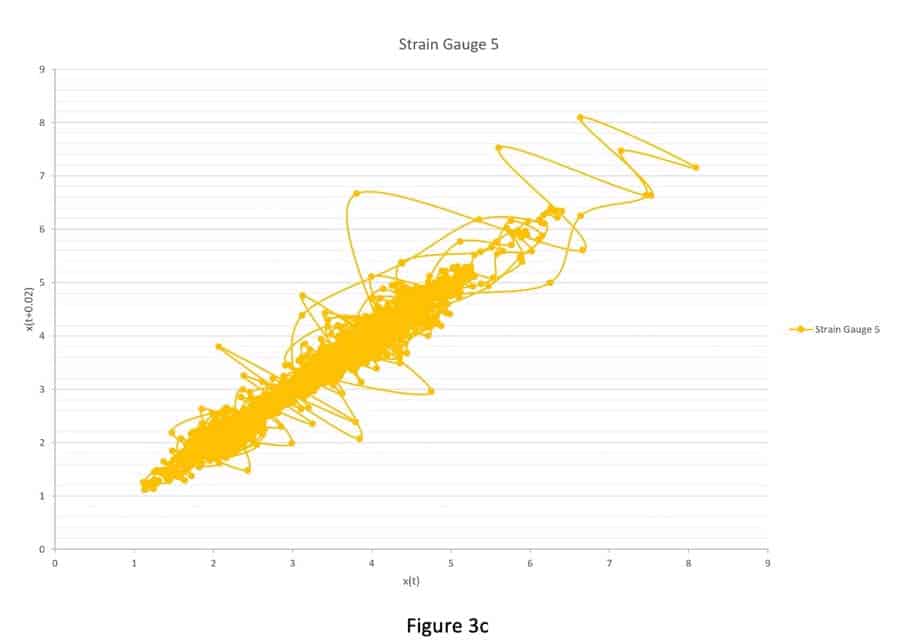


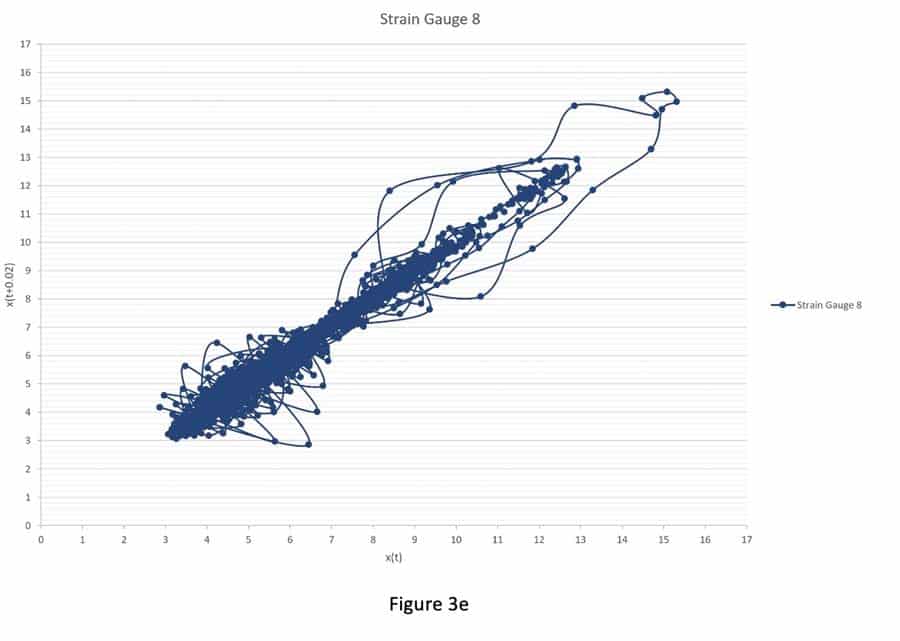
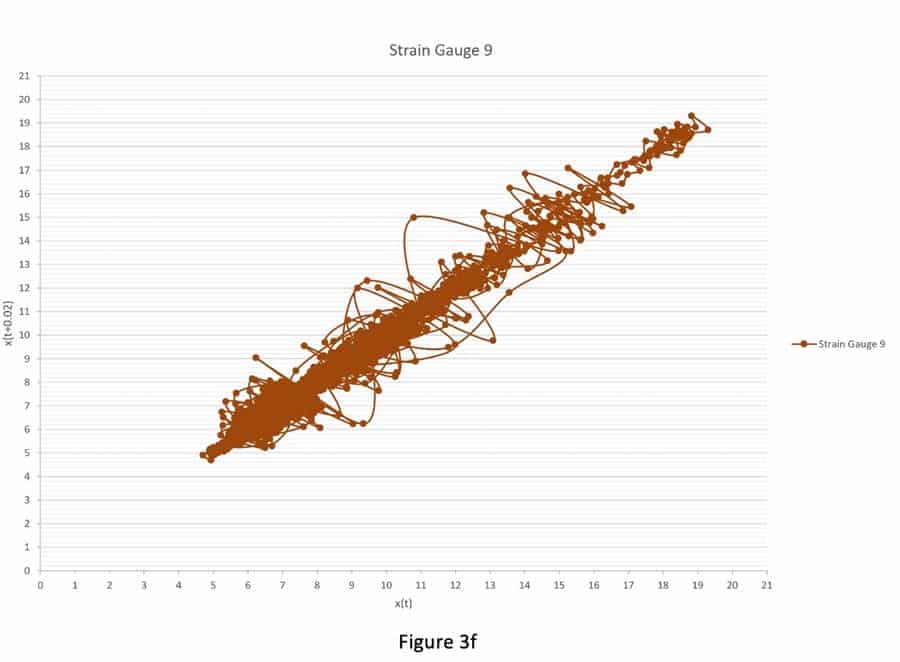
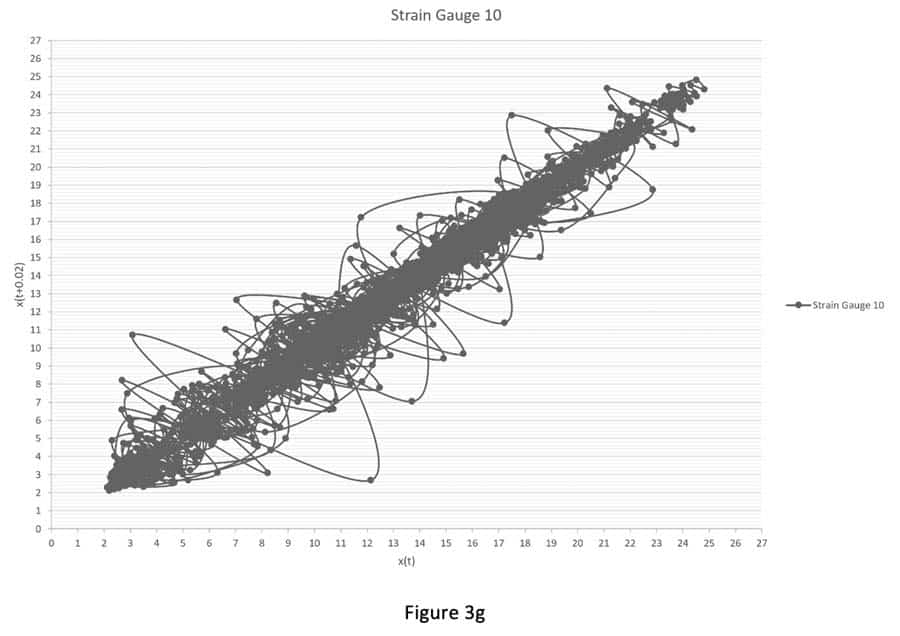
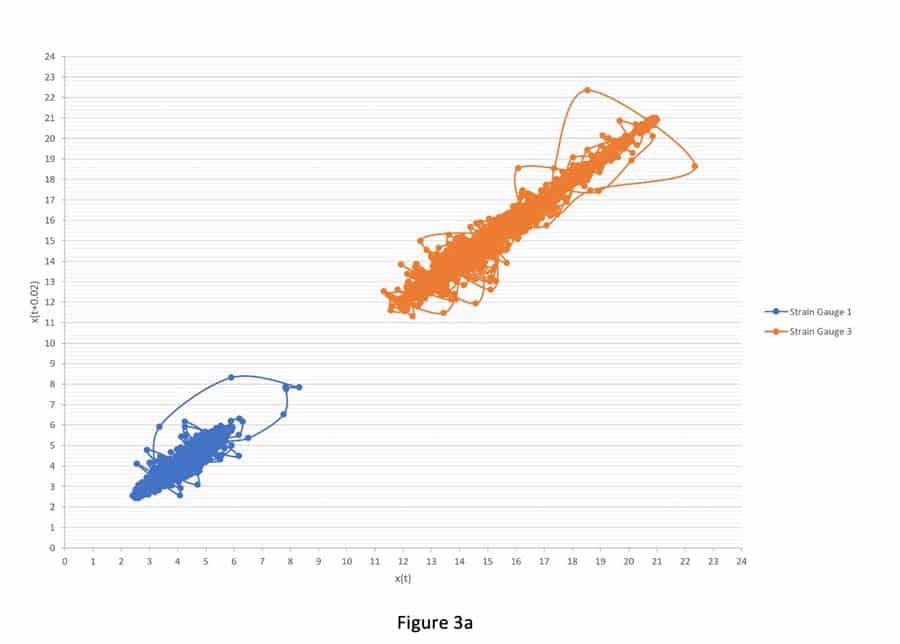
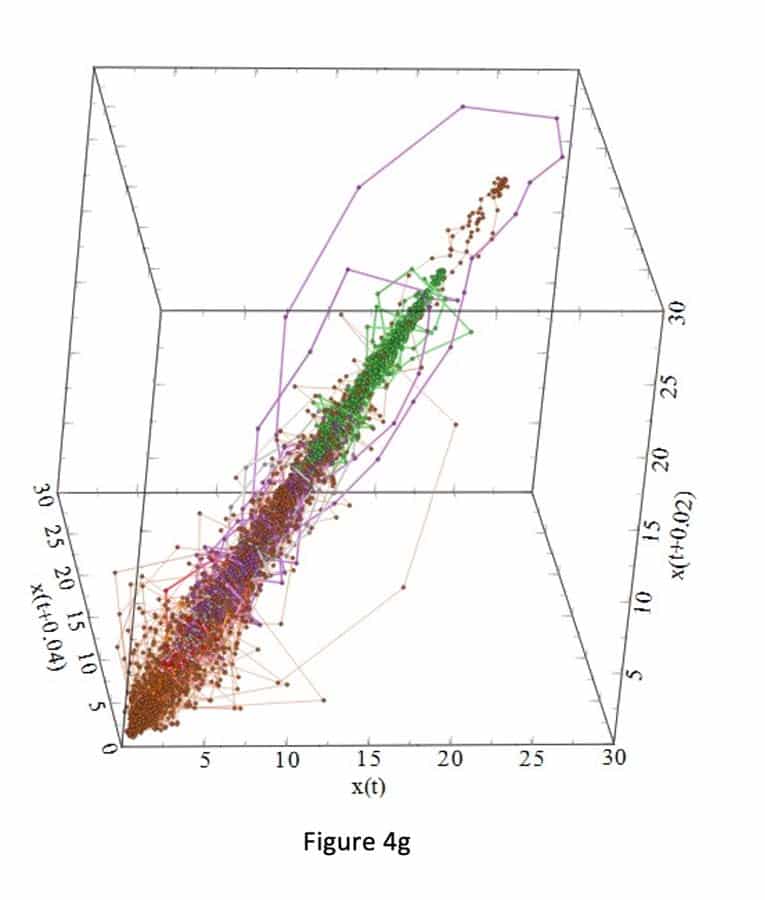
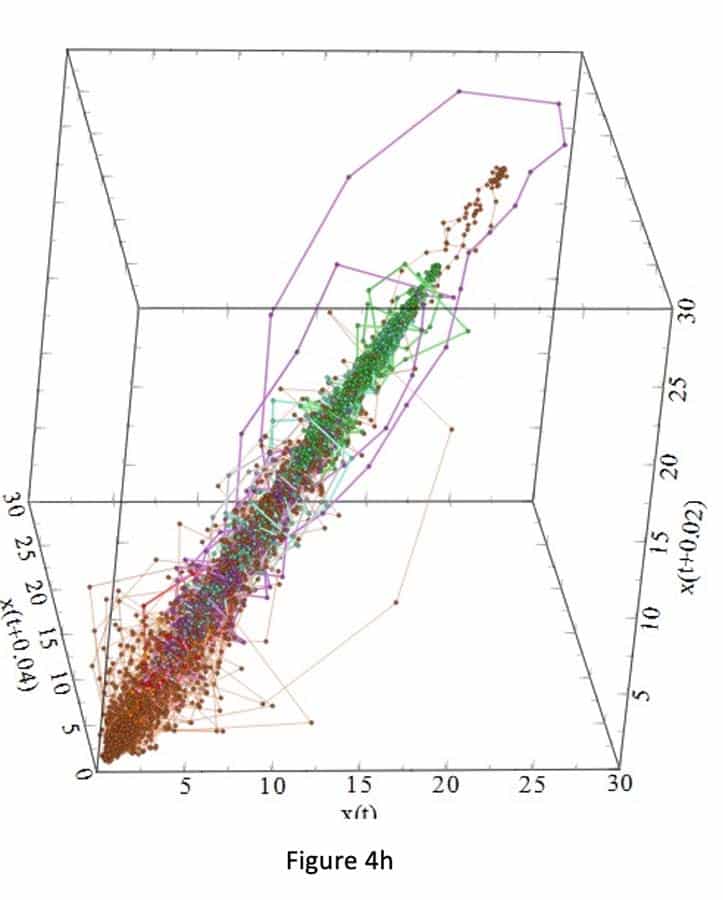
Figures 3a-i and 4a-i suggest that the behavior of the attractors for the gauges behave differently, because it depends on the locations (initial condition) of the strain gauges in the step, and thus on the sensitivity to passenger loading of the location in the step. For example, Figure 3 shows that the attractors for strain gauges 1 and 3 are not affected by the passenger loading. Passenger loading affected the attractors for strain gauges 4 and 5 in a manner totally different from the attractors from strain gauge 6. There is good similarity between the attractors for strain gauges 7, 8, 9 and 10: their loop sizes are progressively bigger, compared to the attractors for strain gauges 1 and 3.


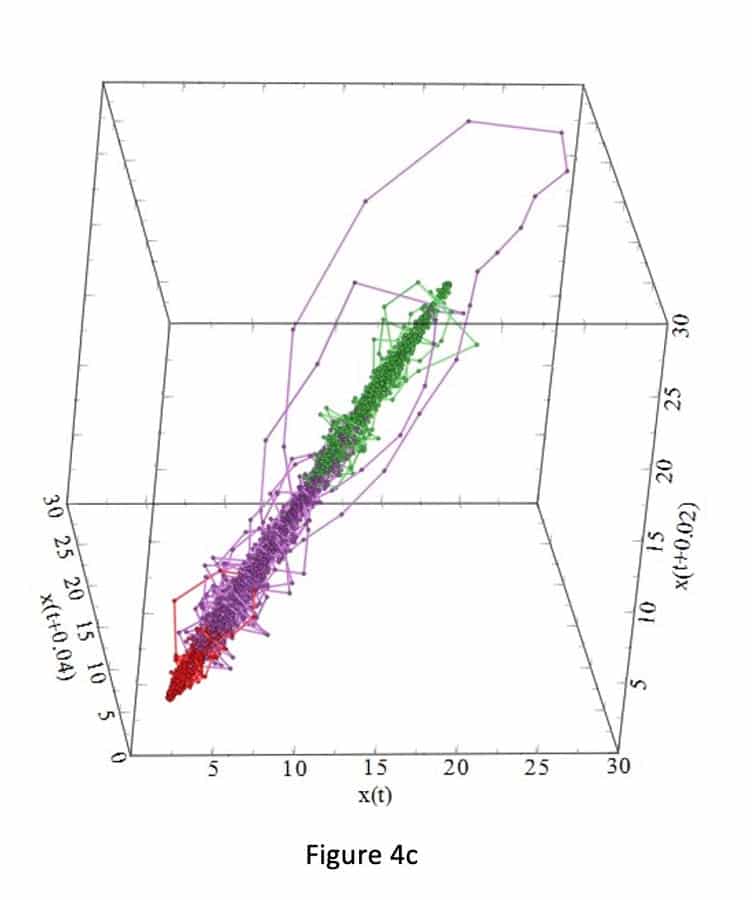
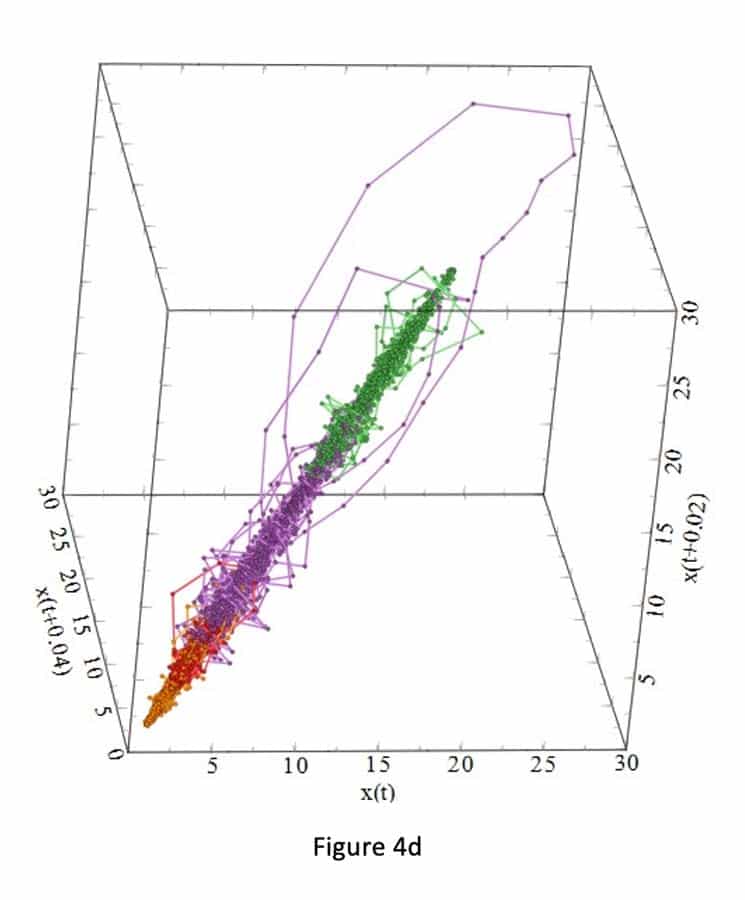

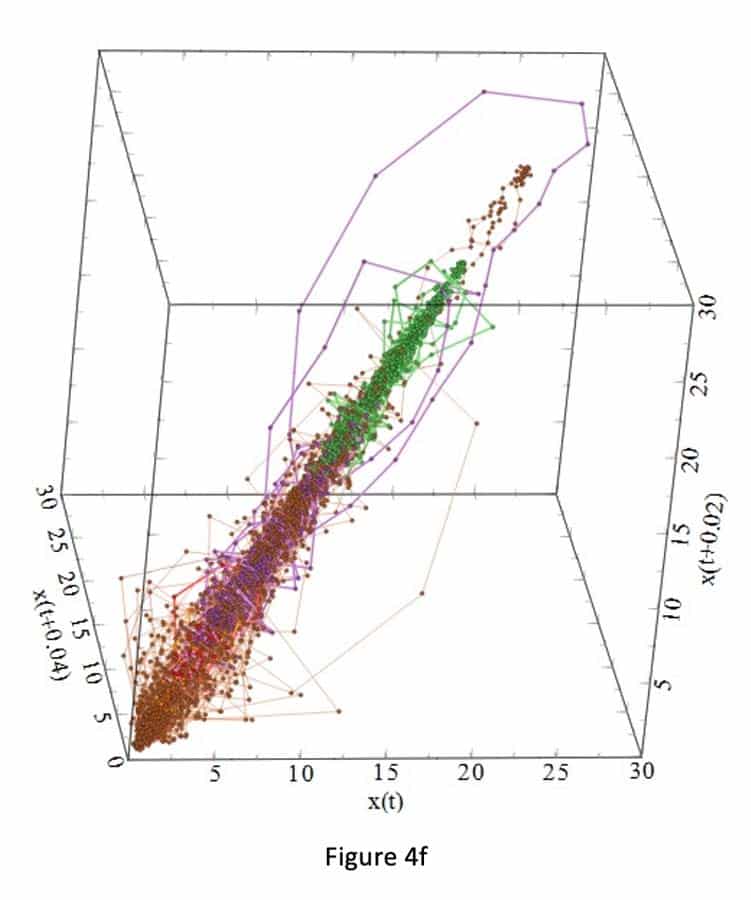

Conclusions
The deterministic nature of the attractors of measurements from the smart step has been reconfirmed in this study, even with the effect of passenger loading. The attractors have represented themselves in closed periodic loops that reflect a steady oscillation motion. Passenger loading has caused the oscillations for some attractors of some strain gauges to be wider and bigger than the cause without the effect of passenger loading.
Parts 1 and 2 of this study have shown that Poincare map and phase space map can be a valuable tool in detecting the behavior of a machine like an escalator with and without the effect of passenger loading. In the next study, we will try to quantify the effect of malfunctions in a machine like an escalator. We will try to answer the question, “Would the technique of using Poincare map and phase plan map be good enough to recognize and categorize malfunctions in the machine?”
References
[1] Ali Albadri, “The construction of Poincare Space Map and Phase Plan Map For Escalators (Part 1).”
[2] W. Zhao, M Li, L. Xian, Hindawi Publishing Cooperation, “Shack & Vibration,” vol. 2015, p.18.
[3] Z.G. Wang, “Dynamic modelling and response analysis to impact of elastic floating raft system,” Journal of Ship Mechanics, vol. 9, no. 6, pp. 113-125, 2005.
[4] Pravin Singru, Vishnuvardhan Krishnakumar, Dwarkesh Natarajan, Ayush Raizada, Department of Mechanical Engineering, K.K. Birla Goa Campus, Goa, 403726, India.
[5] “Chaotic Vibration,” Francis C. Moon, 2004. “Introductory Remarks,” in Dimensions and Entropies in Chaotic Systems, G. Mayer-Kress, Springer-Verlag, Berlin.
[6] “Frequency Demultiplication,” Nature 120 (3019), 363-364. “Nonlinear Dynamics and Chaos,” J.M.T. Thompson and H.B. Stewart, 1987.
[7] “Fractal and Chaos Simplified for The Life Sciences,” Larry S. Liebovitch, 1998.
[8] “Complexity: A Guided Tour,” Melanie Mitchell, 2009.
[9] “Symbolic Dynamics of One-Dimensional Maps: Entropies, Finite Precursor, and Noise,” Crutchfield J.P., and Packard N.H, Int. J. Theor. Phs., 21(6/7), 433-465.
[10] “Theory and Applications of Cellular Automata,” Wolfram S., World Scientific Publ., Singapore.
[11] “Tube Lines Gets Smart to Monitor Escalator Wear,” A. Albadri, ComputerWeekly.com, 07/01/2008.
[12] “Measuring Escalator Heartbeat,” A. Albadri, Elevators, Due to be published.
[13] “Escalator Fractal Behavior,” A. Albadri, Elevators, Due to be published.
[14] “Evidence of Homoclinic Orbits as Precursor to Chaos in a Magnetic Pendulum,” Moon F.C., Cusumano J., and Holmes P.J., Physica D, 1987.
[15] “Experimental Models for Strange Attractor Vibration in Elastic Systems,” Moon F.C., Holmes P.J. in New Approaches to Nonlinear Problems in Dynamics, pp. 487-495, 1980b.
[16] “Period Doubling and Chaotic Behavior in a Driven Toda Oscillator,” Klinker T., Meyer-Ilse X., and Lauterborn W., Phys. Lett. A 101(8), 371-375, 1984.
Get more of Elevator World. Sign up for our free e-newsletter.









