Applied Research on Office Building Elevator Configuration
Jun 1, 2015

A case study illustrates that the CMOPSO algorithm method is better than the traditional elevator configuration method of improving the service quality of office buildings.
by Ma Lianzhe, Luo Zhiqun, Huang Shaolun and Wan Jianru
As the number of high-rise office buildings continuously increases, it is more and more obvious that elevator configuration is an important issue.[1] However, the traditional elevator configuration method can hardly meet the requirements of the modern elevator traffic system. A multi-objective optimized mathematical model of elevator configuration called the “Chaotic Multi-Objective Particle Swarm Optimization (CMOPSO)” algorithm has been established to solve this problem. An elevator configuration application system has been designed by the hybrid programming technology of Visual Basic (VB) and MATLAB.
Due to elevators’ differences from horizontal transportation equipment, it is very difficult for elevators to be added or modified after their installation and utilization. Therefore, designers must pay more attention to elevator configuration when designing the building. Reasonable elevator traffic configuration can make full use of office building space, allocate crowd flow effectively and save energy. Conversely, unreasonable elevator traffic configuration not only increases crowdedness and/or the cost of elevators, but also reduces the effective utilization of building space.[2]
Many variables of an elevator system should be considered in the process of elevator configuration. The traditional elevator configuration method usually applies trial and error according to statistical formulae. This method both takes too much time (for it requires repeated iteration) and is imprecise in the control of costs or shortening of the average waiting time. Therefore, based on the basic parameters and principles of elevator configuration, the CMOPSO algorithm application system offers good interface expressiveness due to having been designed in VB. The configuration scheme transfers the complex and tedious manual iterative calculation to a computerized automatic operation, thus greatly reducing operation time and effort; while effectively reducing average waiting time, both for the up-peak and down-peak.
Elevator Configuration
“Elevator configuration” refers to the selection and settings of the elevators in the buildings, including rated speed, rated loading capacity, car size and number of units to achieve the purpose of obtaining an optimal price/performance value of the elevator system.
In the process of elevator configuration, not only should the effective utilization of the building space be considered, energy and cost savings should, as well. Elevator configuration should be reasonable in order to improve the service quality of elevator transportation. Therefore, the elevator configuration is a multi-objective optimization problem.
Multi-Objective Optimized Elevator Configuration Model
Independent Variables
The independent variables of the multi-objective optimized elevator configuration model include: Re (rated load), V (rated speed), N (number of elevators), M (elevator service region), r (number of passengers in one cycle) and ae (rated acceleration).
Multi-Objective Functions
The three basic principles of optimal elevator configuration are:
- Elevator service running time, which is used to indicate the quality of elevator service, should be as short as possible and that average waiting time is used as the main performance indicator.
- The number of elevators is reasonable.
- Energy savings
The elevators of the office building are divided into M regions. The elevator running time (Fk) of the kth (1 ≤ k ≤ M) region is represented by the reciprocal of passengers’ arrival rate within a period of 1 s. Supposing there are Nk elevators in the kth region:
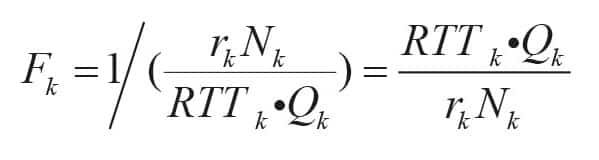
To achieve the first principle, Equation 2 should produce a minimal value.
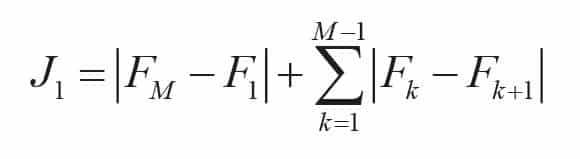
To achieve the goal of reasonable number of elevators, Equation 3 should also get a minimal value.

To achieve the object of energy savings, suppose that the balance coefficient of the elevator is øk(0.4~0.5), the total mechanical transmission efficiency of the elevator is ŋ, the computing time is T, then the energy consumption of the elevators in the kth region is:
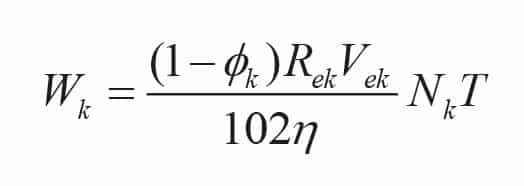
Then, the third objective function is:

Considering the mutual influence and mutual restraint relationship between the three objectives, only making one objective function get minimal value does not work. So, making the overall objective function get the minimum is the way to obtain the optimal scheme of elevator configuration. Weighting factor λi is introduced, and the overall multi-objective function is shown in Equation 6. It can be concluded that the optimal elevator configuration scheme is established as long as the optimal solution of Equation 6 is obtained.

Constraint Equations
The average interval time (AIk) of the kth set of elevators should satisfy the following constraint equation:
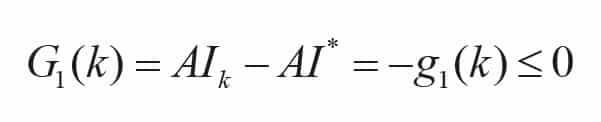
In the process of elevator configuration, as long as CE ≥ CEa is satisfied, the transport efficiency of the elevator traffic system can meet the requirements. So, the following constraint equation (Equation 8) is established.
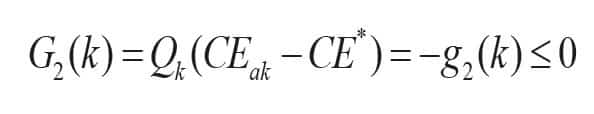
where CE represents the passengers’ arrival rate within 5 min., and CEa is the passengers’ arrival rate within 5 min. during the peak of passenger flow.
Assuming that the expected average travel time (AP) is 120 s. to the limit and the expected average waiting time (AWT) is 45 s. to the limit, the following constraint equation is established.

where g1(k), g2(k) and g3(k) are small positive numbers (in seconds).
Optimal Elevator Configuration Algorithms
MOPSO
The Multi-Objective Particle Swarm Optimization (MOPSO) algorithm generates the initial swarm randomly and conducts multiple iterations. In each iteration, each particle updates its speed and position by the personal optimal solution (pbest) and global optimal solution (gbest) — the optimal solution found by the entire swarm. Finally, the optimal solution of the multi-objective optimization problem is found through multiple iterations.[3] In MOPSO, each particle is a solution of the d-dimensional optimized space, and its quality is decided by the fitness value of the multi-objective function to be optimized.[4]
Suppose that there are m particles in the swarm, in the tth ordered iteration. The location of the particle is expressed as Xi(t) = (Xi1(t), Xi2(t), . . . Xid(t)); the speed of the particle is expressed as Vi(t) = (Vi1(t), Vi2(t), . . . Vid(t)); the optimal solution found by the particle itself is expressed as Pi(t) = (Pi1(t), Pi2(t), . . . Pid(t)); and the global optimal solution is expressed as Pg(t) = (Pg1(t), Pg2(t), . . . Pgd(t)). In the tth ordered iteration, the particle updates its speed and location according to the following equations:


where w represents inertia weight. It can balance the search capability of the group. c1 and c2 are learning factors and nonnegative constants. r1 and r2 are mutually independent random numbers that belong to [0,1]. i = 1, 2 . . . m. j = 1, 2, . . . d.
Although the particle swarm optimization (PSO) algorithm can obtain good results in solving multi-objective optimized problems, the particles are prone to prematurely converge to the local optimum in the process of evolution, due to the randomness of the particles in the process of initialization and evolution. Therefore, in this paper, the idea of chaos is applied to the PSO algorithm in order to improve its quality.
Chaotic MOPSO (CMOPSO)
Chaos is a general phenomenon in nonlinear systems.[5] The chaos optimization theory is applied to the PSO algorithm by taking advantage of the ergodicity of chaotic motion. The CMOPSO algorithm can overcome the shortcomings of the PSO algorithm, namely premature convergence and local optimum. Meanwhile, it can increase the convergence speed and accuracy of the PSO algorithm.
The following logistic equation is introduced to the PSO algorithm to realize the combination of the chaos idea and PSO algorithm:

where μ represents the control variable. Suppose that μ = 4 and 0 ≤ z0 ≤ 1 — then, the system is completely in a state of chaos. A certain time sequence (z1, z2, z3. . .) can be iterated by the random initial value z0∈[0,1]. Then, the position and speed of the particles are initialized by chaotic sequence, and one particle in the current swarm is replaced by the optimal particle (generated in the chaotic sequence). Therefore, the condition in which the PSO algorithm easily falls into the local optimum is improved.
Algorithm Process
In the CMOPSO algorithm, each particle represents a kind of elevator configuration scheme. According to the independent variables, the multi-objective functions and the constraint equations of the multi-objective optimized elevator configuration model, the elevator configuration program based on CMOPSO algorithm is programmed in MATLAB so as to select the optimal location of the particles, namely the optimal elevator configuration scheme. The algorithm process is outlined in the following steps:[6]
Determine the objective functions and constraint equations of the
1) multi-objective optimized elevator configuration.


2) Initialize the maximum allowable number of iterations or fitness error, inertia weight and learning factor of CMOPSO.
3) Initialize the position and speed of the particles by the chaos idea. An m-dimensional vector is randomly generated, and each component is valued from 0 to 1, namely z1 = (z11, z12, . . . z1d). d is the number of the independent variables in the objective functions. In this article, d = 6. According to the chaotic system, m vectors are obtained, and each component of zi is carried to the corresponding value interval. Then, the fitness value of the particle swarm is calculated, and x solutions with better performance are chosen from the swarm to be the initial solutions. Then, x initial velocities are randomly generated.
4) If the fitness value of the particle is superior to the personal optimal solution, pbest is set as the best position.
5) If the fitness value of the particle is superior to the global optimal solution, gbest is set as the best position. Then, the speed and position of the particles are updated respectively.
6) The optimal position Pg(t)=(Pg1(t), Pg2(t),… Pgd(t)) is optimized by chaos, then, the feasible solution that has the best performance (P*) is obtained.
7) Replace of the position of any particle in the current swarm with P*.
8) If the CMOPSO algorithm meets the stop condition (the performance indicators of the elevator configuration), the elevator configuration system will stop searching and output the global optimal solution. Otherwise, return to step 4.
According to the CMOPSO algorithm, the application system of optimal elevator configuration is designed by the hybrid programming technology of VB and MATLAB.
Configuration Interface
Input Interface of Basic Parameters
First, the user can set up the parameters through the input interface. This includes inputting the total area of the building (U), the effective area of the building (S), the number of people receiving the elevator service (Q), service layers of the elevators (n), height of the building (H) and the expected AWT. Then, the system will automatically set the elevator parameters, such as rated speed (V) and rated loading capacity Re.
Output Interface of Configuration Results
The elevator configuration system operates the program in the background of the interface according to the above principles of elevator configuration. It then outputs the results of the elevator configuration.
Performance-Evaluation Interface
According to the results of the elevator configuration, this interface can calculate and output various performance indicators, including AWT, up-peak AWT (AWTu) and down-peak AWT (AWTd). The average waiting time is chosen as the main performance-evaluation indicator. The design process of the elevator configuration is illustrated in Figure 1.
Figure 1: The elevator configuration design process: Sa is the acceleration distance, tr is the single-floor flight time, td is the door-opening/-closing time, tp is the passenger transfer time, and RTT is the round-trip time.
Elevator Configuration Case Study
Take a modern high-rise office building with a total area of 30,000 m2, effective area of 27,000 m2, 24 layers (floors)/78 m tall, 3,000 users and an expected average waiting time of 45 s. The interface, after inputting the basic parameters, is shown in Figure 2.
Figure 2: Input interface with basic parameters
According to the above parameters, the elevator configuration is conducted by the configuration scheme based on CMOPSO algorithm and the traditional configuration scheme, respectively. The performance parameters of the elevators configured by CMOPSO are the rated loading capacity of 1350 kg and rated speed of 2.5 mps (Figure 2). The configuration results of the CMOPSO and traditional schemes are shown in Figures 3 and 4.
Figure 3: The CMOPSO scheme results
Figure 4: The traditional scheme results
Table 1: Comparison of the CMOPSO and traditional schemes
From Table 1, compared with the traditional elevator configuration scheme, the elevator configuration scheme based on the CMOPSO algorithm reduced the average, up-peak average and down-peak AWTs. This is because the CMOPSO method can find the optimal solution through fast multiple iterations and control the independent variables more accurately, thus providing more reasonable elevator selection and settings. The result shows that the elevator configuration scheme based on the CMOPSO algorithm is more effective in elevator configuration.
Conclusion
The CMOPSO algorithm and an elevator configuration application system have been presented. The case study shows that the elevator configuration scheme based on the CMOPSO algorithm can effectively reduce the average, up-peak average and down-peak average waiting time, thus improving the service quality of an office building. Thereby, the elevator configuration scheme based on the CMOPSO algorithm provides a feasible and effective solution for elevator configuration.
Acknowledgement
This research was supported by AQSIQ Nonprofit Industry Specialized Research Funding (No. 201310153).
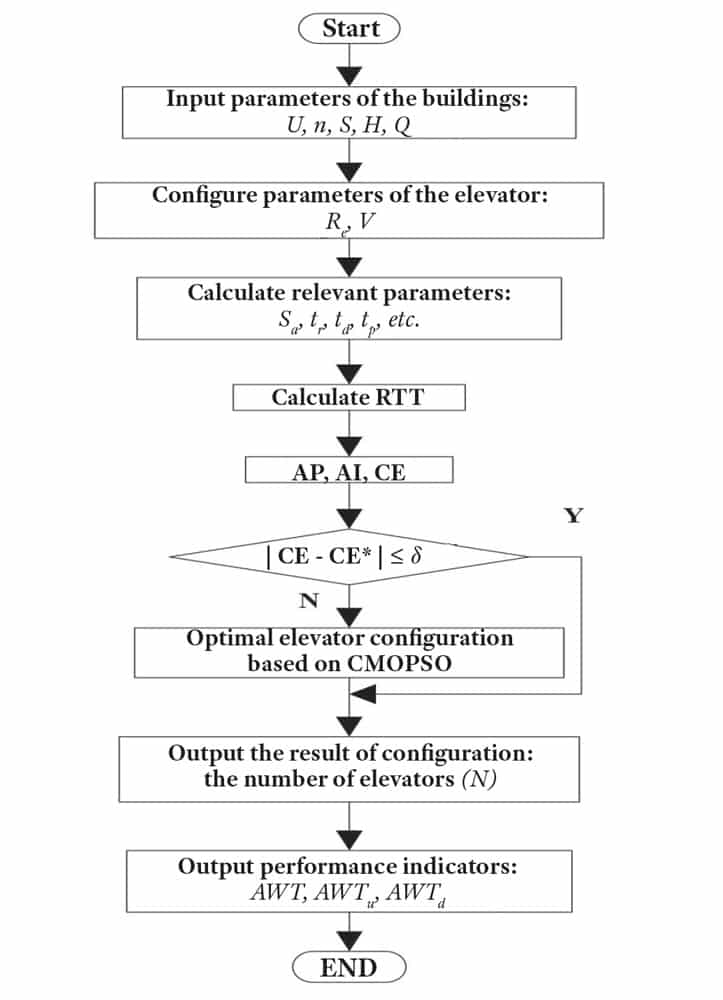
Figure 1: The elevator configuration design process: Sa is the acceleration distance, tr is the single-floor flight time, td is the door-opening/-closing time, tp is the passenger transfer time, and RTT is the round-trip time. 
Figure 3: The CMOPSO scheme results 
Figure 4: The traditional scheme results 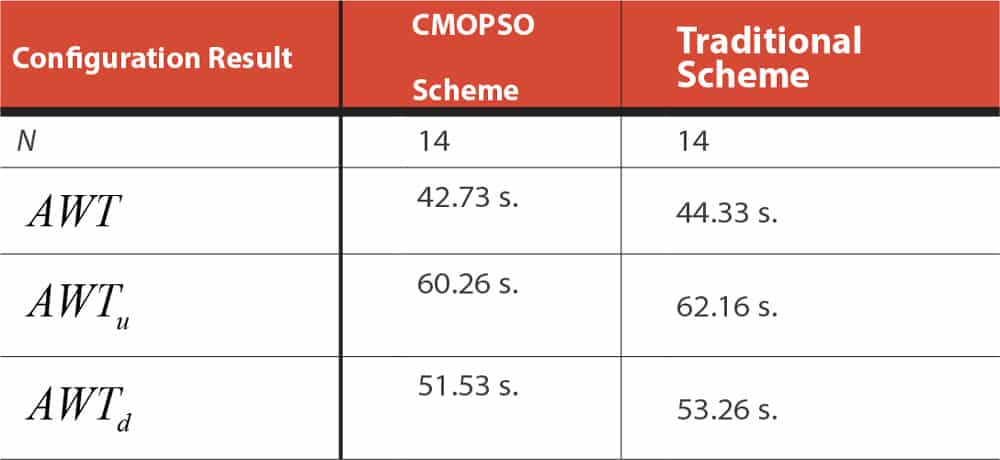
Table 1: Comparison of the CMOPSO and traditional schemes
References
[1] Zhu Lin, Jiang Qing, Cao Jie and Wan Jianru. “Elevator Group Control Method,” ELEVATOR WORLD, 2013, 11:46-54.
[2] Zhang Junli. “Elevator Traffic Dispatching and Its Software Development.” South China University of Technology, Guangzhou, China, 2012 (in Chinese).
[3] Qian Huang, Tianwei Li, Zhengyou Li and Yundong Hang. “Research on PID Control Technique for Chaotic Ship Steering Based on Dynamic Chaos Particle Swarm Optimization Algorithm.” 10th World Congress on Intelligent Control and Automation (WCICA 2012): 1639-43, 2012.
[4] Shen Hong. “Research on Compensation Technology of Current Harmonic and Voltage Sag in UPQC.” Tianjin University, Tianjin, China, 2009 (in Chinese).
[5] Li Shuang, Wang Zhixin and Wang Guoqiang. “Application of an Improved PSO-Based PID Neural Network Controller for VSC-HVDC.” Proceedings of the CSEE, 2013, 33(3): 14-21 (in Chinese).
[6] Pan Feng, Li Weixing and Gao Qi. “Particle Swarm Optimizer and Multi-Object Optimization.” Beijing Institute of Technology Press, Beijing, China, 2013 (in Chinese).
Get more of Elevator World. Sign up for our free e-newsletter.








