Translating the heartbeat of the escalator
Measuring the behaviour of an escalator from measured signals collected from various parts of the machine is an interesting and useful concept. Behaviour of an escalator can be measured by using the smart step. The smart step measures the fingerprint or the heartbeat of the machine. Any anomalies in the behaviour of the escalator, such as a developing mechanical failure, will be shown in the traces for the heartbeat.
We established in our previous studies that the heartbeat of an escalator has fractal characteristics.[1-6] The heartbeat of the escalator can be translated to a single value in the form of the fractal dimension. It is a detection technique that can detect the health and fitness of the machine. The principle of this work is not limited to escalators; it can be applied to any electro-mechanical machine.
This study will look into the behaviour of temperature distribution in a gearbox for an escalator. It asks and answers the following questions:
- Does the temperature of the escalator gearbox have fractal behaviour or characteristics?
- Can the fractal behaviour of the gearbox be quantified?
- Would the values of the fractal dimension for the gearbox give an insight into the mechanical behaviour of the escalator, such as disclosing potential of failures and malfunctions?
Introduction
We have proven that the smart step can measure the heartbeat of the escalator.[1] The heartbeat can be translated into a single value in the shape of the fractal dimension, Df.[2-6] The values of the fractal dimension were measured by measuring the stress levels in different locations in the smart step.[2-6] These values can be used as an indicator of the operation quality of the machine. They can also predict potential failures in the escalator.
In this study, our attention will be on the temperature distribution in the escalator gearbox (Figure 1). Although nonlinear behaviour of machines and their individual components have been studied,[7] to our knowledge there has never been a study similar to our approach in this study; therefore, not a lot of research is available to address the three questions we stated above.
Temperature Data Collection
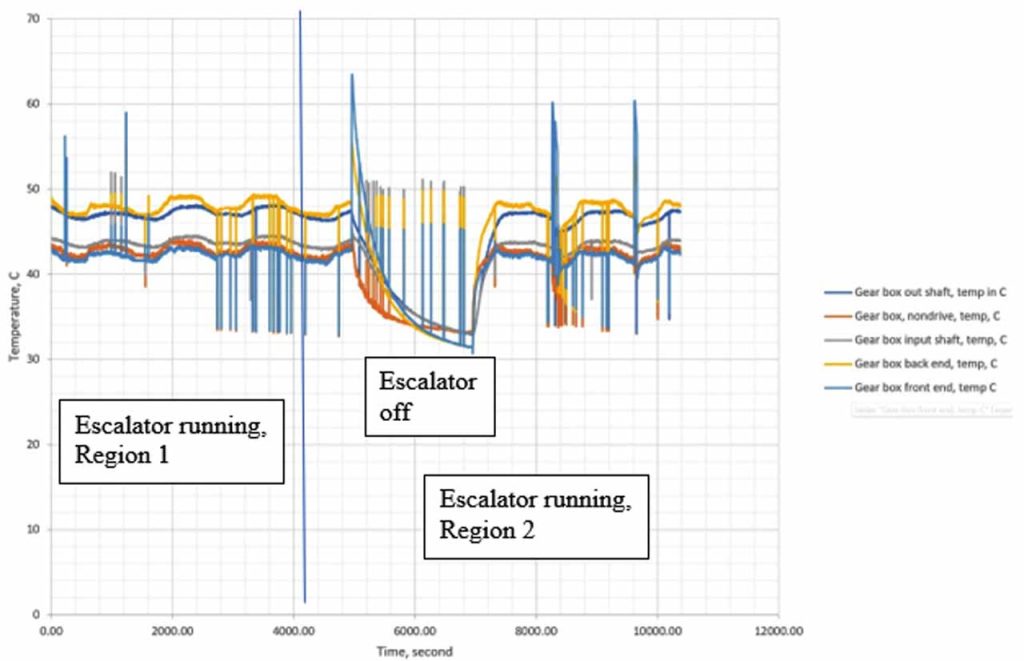
Temperature sensors were distributed at different locations on the gearbox, as shown in Figure 1. The data/traces were logged into a data logger, (Figure 2), then downloaded to a computer for analysis. The period of runs was divided into two regions: region 1 and 2. Region 2 includes a shutdown period to impose a stage of variation in the measurements. It is our intention to see whether the adopted technique of determining the fractal dimension will or will not detect this variation.
Methodology Used To Determine Df (Fractal Dimension)
The scaling step technique has been used here to determine Df. A computer program was written in Microsoft Excel to determine Df and plot the data. Our methodology is very similar to the Multiresolution Length Method, which has been used by many researchers.[8-10]
The steps in the time series = s = {s(0), s(1), s(2), s(3) . . . s(n)} of length n of the trance. Each point in the plot is represented in (xi, yi) when i = 1, 2, 3 . . . n. xi values are abscissa, and yi values are ordinate values. The Euclidean distance between two points (x1, y1) and (x2, y2) is:
dist(s1, s2) = ((x1 – x2)2 + (y1 – y2)2)0.5 (1)
The total length of the curve of the first-time resolution is calculated as:
L = I = 1∑n – 1 dist(si, si + 1) (2)
It is noted that, as the resolution becomes coarser, the estimated length of the time series becomes less accurate. Repeat the above for different resolutions, r = r1, r2, r3, r4 . . . rp, where rp is the maximum coarsest resolution at which the length of the curve is calculated.
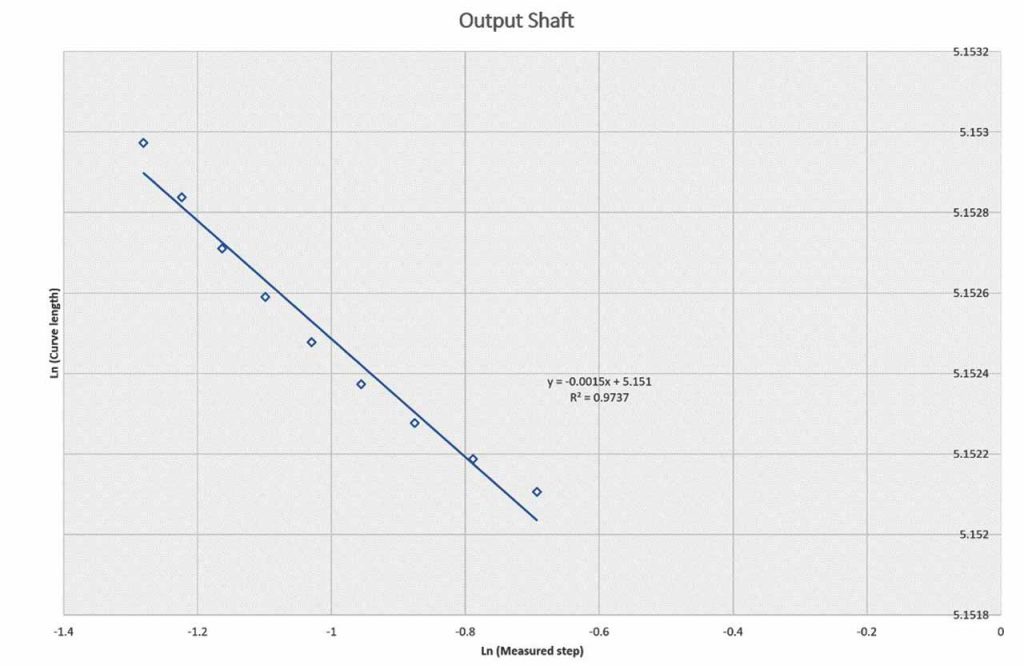
By drawing a log-log graph (1/rk) versus (Lr) and computing the slope, the fractal dimension is calculated from:
(Df – 1) = -[log(Lr)/log(1/rk)] = -[slope] (3)
Temperature distribution sensors were located at different places on an escalator gearbox (Figure 1).
Figure 2 shows the traces of temperature against the running time for the escalator.
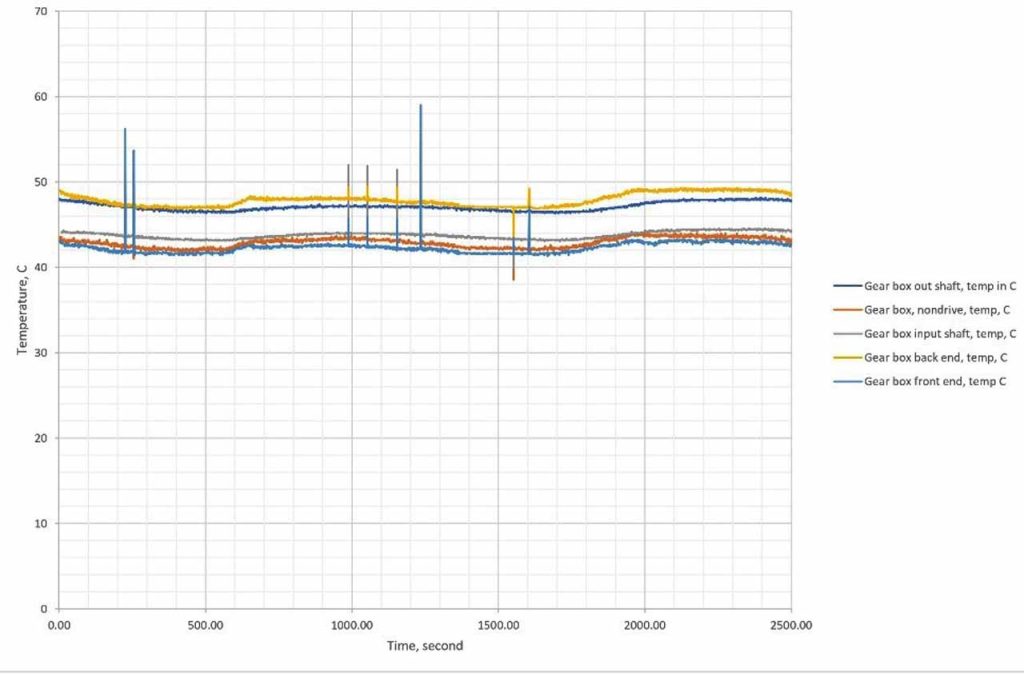
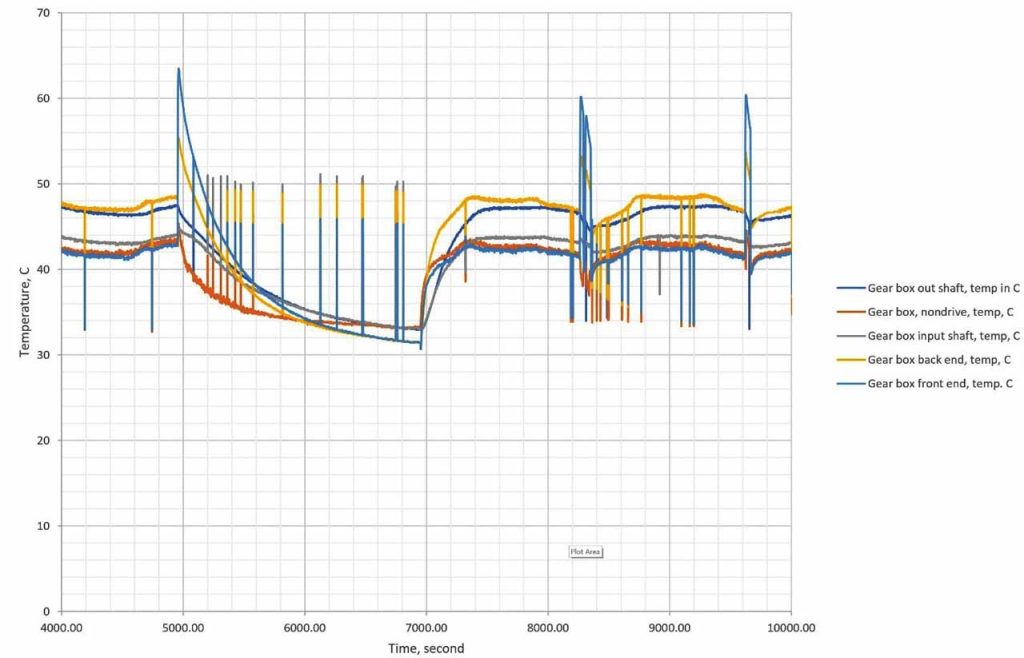
Figure 3 presented a magnification view to regions 1 and 2, shown in Figure 2.
Results and Discussion
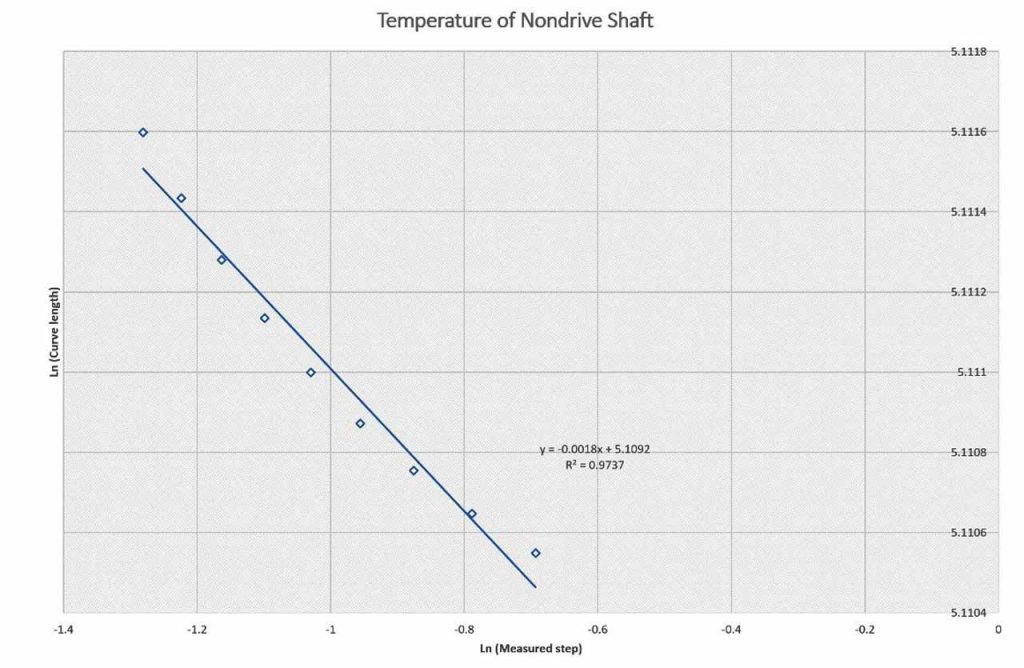
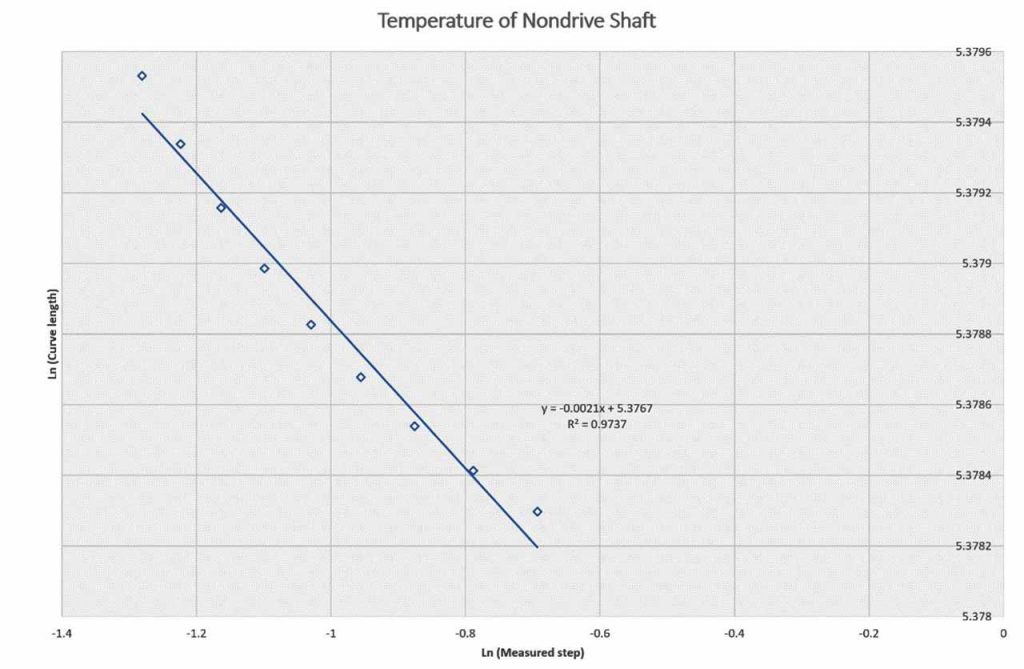
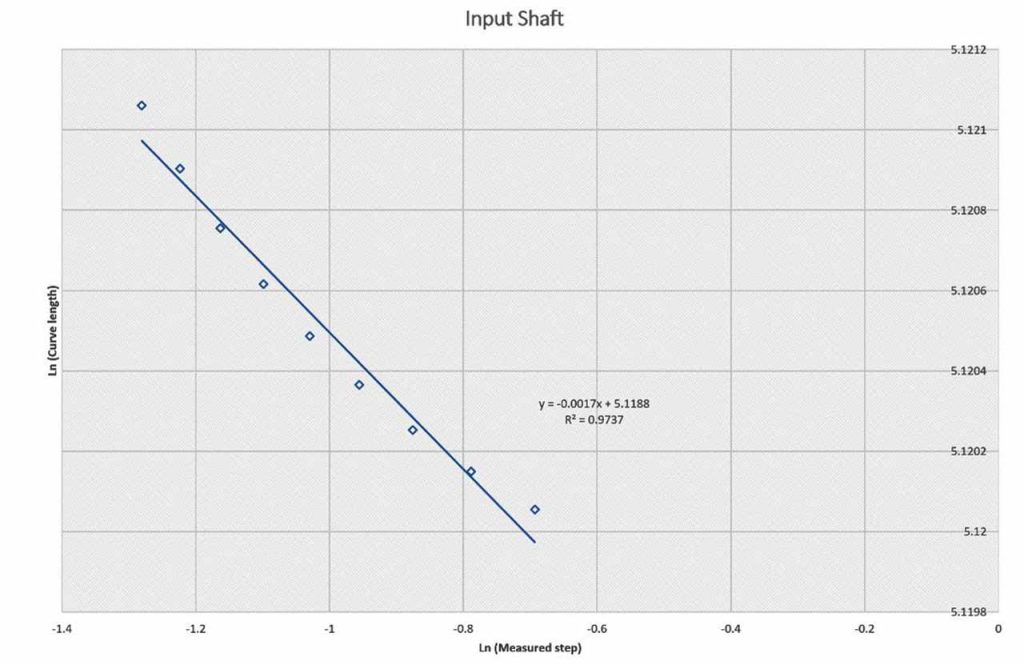
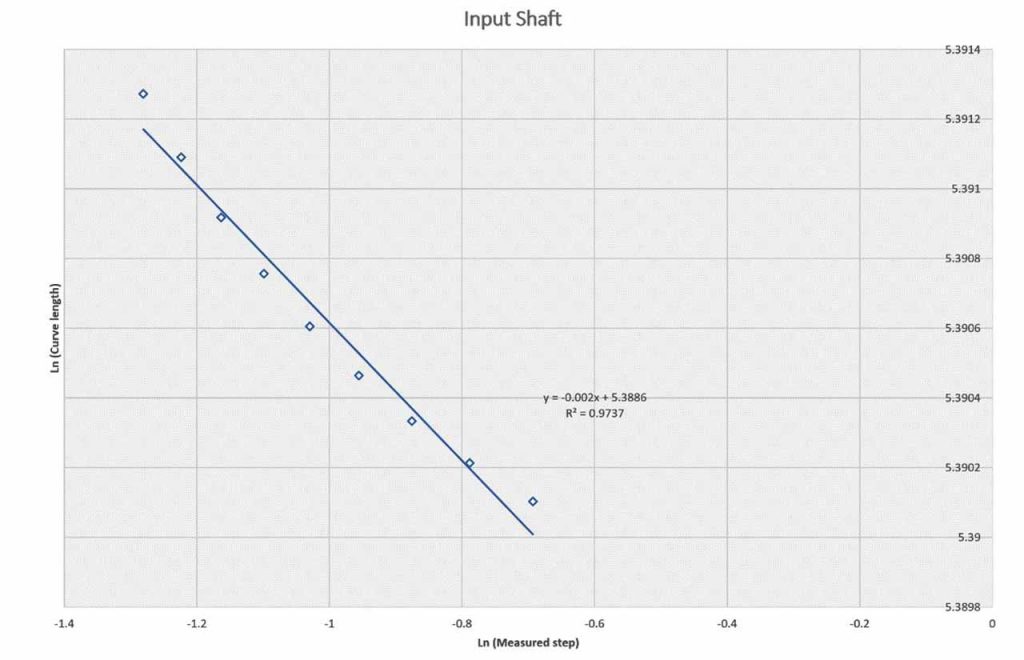
| No | Temperature Trace Type | Fractal Dimension value, Df (0.0-4,000 s) | Fractal Dimension value, Df (4,000-10,000 s) |
| 1. | Output gearbox shaft | 1.0015 | 1.0018 |
| 2. | Nondrive gearbox shaft | 1.0018 | 1.0021 |
| 3. | Input gearbox shaft | 1.0017 | 1.002 |
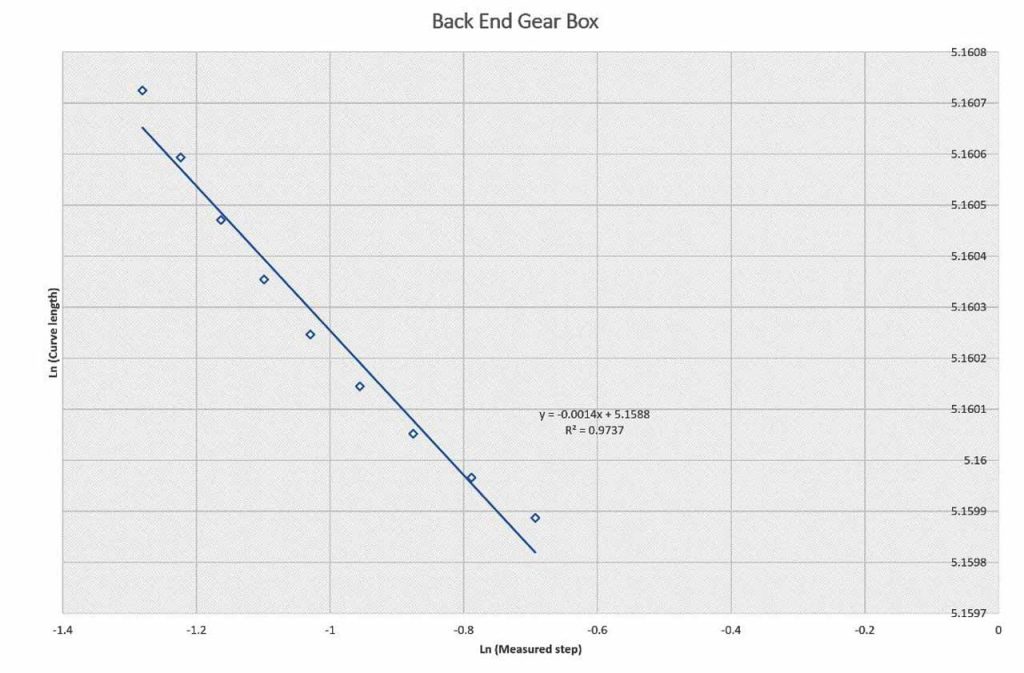
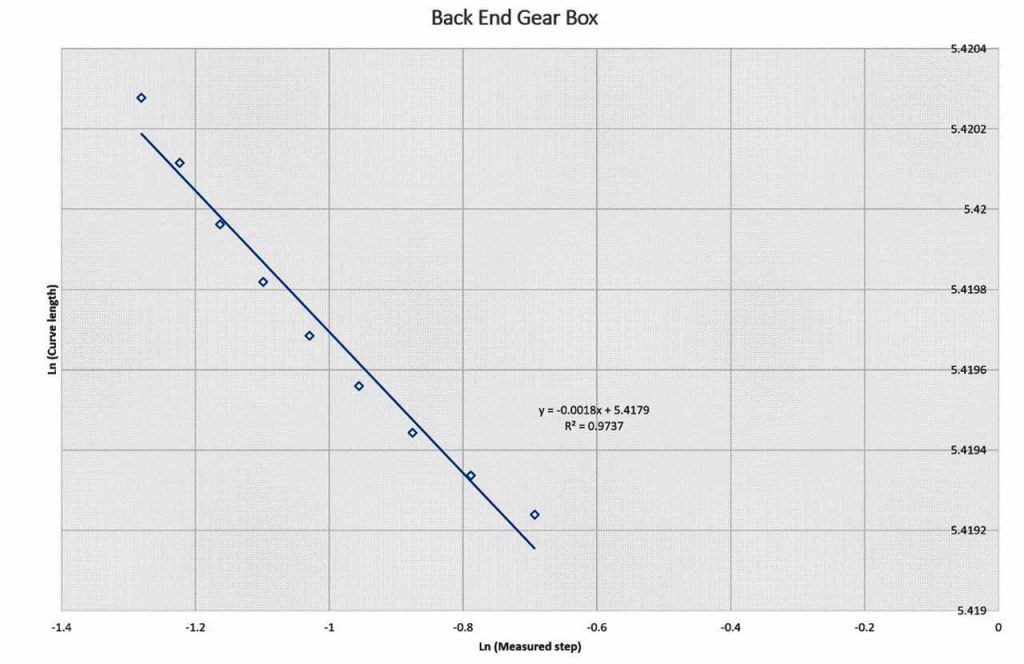
| 4. | Back gearbox shaft | 1.0014 | 1.0021 |
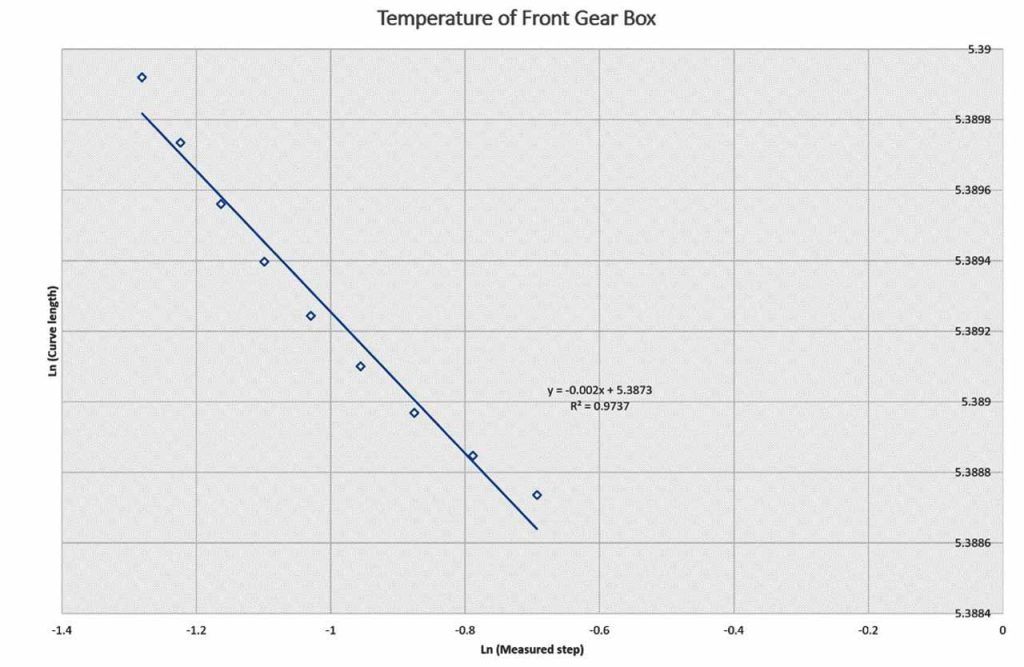
| 4. | Front End gearbox shaft | 1.0017 | 1.002 |
Table 1 and Figures 4, 5, 6, 7 and 8 present the fractal dimension values for the traces of the measured temperatures from different locations in the gearbox. The roughness of the traces in Figure 3 shows that, in general, they are smooth, except some drops out in the signals. Table 1 lists the estimated fractal dimension values for the traces. The values reconfirm that all of the traces are smooth, except there are very small variations, which could have been developed as result of the drop outs. The period between 4000-10,000 s has shown higher fractal dimension values than the period 0.0-4,000 s. This could be due to the escalator shutting down, as shown in Figure 2.


Conclusions
The roughness and smoothness of temperature traces, which are measured from an escalator gearbox, can be quantified in the form of fractal dimension values. They can be used to monitor and observe the behaviour of the gearbox during its daily operation. One or two sensors are more than enough to show the overall behaviour of the gearbox during operation. This could have significant advantages, including:
- Monitoring the performance of the gearbox by defining trends.
- Improving maintenance plans by knowing the right time for maintenance and by allocating the right manpower.
- The fractal dimension values that are measured for the gearbox can be connected with the fractal dimension values measured from other parts and assemblies of the escalator. This can be used to deduce the interaction relationships in the behaviour of the gearbox and other components/assemblies in the machine.
- The principles and implications of the technique used in this study can be used in any mechanical system other than escalators.
References
[1] A. Albadri.“Tube Lines Get Smart to Monitor Escalator Wear,” Computer Weekly (07/01/2008).
[2] A. Albadri.“Smart Step Measures Escalators Heartbeats,” ELEVATOR WORLD UK, iss. 104, 20/03/2020.
[3] A. Albadri.“Escalator Fractal Behavior (part 3)”, EW Jan 2021.
[4] A. Albadri.“Smart Step Measures Escalator’s Heartbeat,” EW UK, March-April 2020.
[5] A. Albadri.“Escalator Fractal Behavior (Part 1),” EW June 2020.
[6] A. Albadri.“Escalator Fractal Behavior (part 2),” EW June 2020.
[7] Francis C. Moon, Dynamics and Chaos in Manufacturing Processes,” Wiley Series in Nonlinear Science, 1998.
[8] B.S. Raghavendra and D. Narayana Dutt.“Computing Fractal Dimension of Signals Using Multiresolution Box-Counting Method,” World Academy of Science, Engineering and Technology 37 (2010).
[9] D. Scheianu and I. Tutanescu.“Application of Fractal Signal,” University of Piesti, Communication and Computer Department.
[10] A. Zlatintsi and P. Maragos,Multiscale Fractal Analysis of Musical Instrument Signals With Application to Recognition,” IEEE Transaction on Audio, Speech and Processing, Vol. 21, no. 4 (April 2013).
Get more of Elevator World. Sign up for our free e-newsletter.