Study on the Seismic Response Analysis of Lifting Ropes in the Development of Digital Twin Technology To Reduce Earthquake Disasters in Residential Buildings
Jun 1, 2025

Looking at a way to reduce the most common causes of lift damage during an earthquake
by Keisuke Minagawa, Satoshi Fujita, Takashi Matsushima, Koichi Kajiwara and Toshihiko Horiuchi
This paper was first presented at the 15th Lift & Escalator Technologies Symposium in September 2024 and published at The Lift and Escalator Library.
Keywords: Wire rope, Vibration, Simulation, Seismic response, Earthquake, Digital twin
Abstract
The most common damage to a lift during an earthquake is the rope catching in a piece of internal equipment and a bracket of a hoistway. The natural periods of a building and hoist ropes in the building are usually close, causing resonance, and a large response of the rope is induced. As a result, the rope catching can lead to the confinement of passengers in a car and long-term suspension of lift operation, which has a significant impact on the daily lives of the occupants or residents. To reduce such damage, it is important to estimate the response of the rope by seismic response analysis in advance and to clarify the conditions under which the response of the rope does not increase.
On the other hand, in the field of information technology, the so-called digital twin method has recently been applied. The digital twin is a method of constructing objects that exist in real space in a virtual space and is useful for predicting damage by simulating events such as natural disasters. For rare events such as earthquakes, the application of the digital twin is a very effective method in terms of business continuity planning, evacuation planning and seismic reinforcement. Therefore, the authors’ research team is constructing an earthquake-disaster digital twin for residential buildings.
The earthquake-disaster digital twin requires the construction of analytical models of the ground motion, buildings, furniture, etc., and the authors are constructing an analytical model of lifts, especially the ropes, which are frequently damaged. This paper presents an overview of the method and the results of a seismic response analysis. The method used in this paper is based on the wave equation and takes into account the spatial distribution and time variation of the tension on a rope. The investigation of the conditions under which the response of the rope does not increase during earthquakes is not included in this paper. It will be discussed in the future.
1. Introduction
When a major earthquake, such as the Great East Japan Earthquake in 2011 or the Türkiye–Syria Earthquake in 2023 occurs, buildings and areas can be severely damaged. Even if buildings do not collapse, people’s daily lives are greatly affected by outages of power, water, gas and so on. Damage to lifts caused by earthquakes has been widely reported in the past,[1] and the closure of lifts also has a significant impact on apartment residents due to increasing building heights and an aging society. According to a 2018 Japanese Government survey, the proportion of apartment residential buildings to total housing in Japan was 43.5%.[2] If lifts in apartment residential buildings were damaged by an earthquake, it would have a significant impact on society. Therefore, there are high expectations for damage reduction and early recovery of lifts during and after earthquakes, especially for residential buildings.
In the field of information technology, the so-called digital twin method has recently been developed and widely applied. The digital twin is a method of constructing objects that exist in real space in a virtual space and predicting damage by simulating events such as natural disasters in a virtual space based on the situation of real objects monitored by Internet of Things (IoT) technology and so on. For rare events such as earthquakes, the application of the digital twin is a very effective method in terms of business continuity planning, evacuation planning and seismic reinforcement.
For this reason, the authors’ research team has proposed and is constructing an earthquake-disaster digital twin for residential buildings. The earthquake-disaster digital twin requires the construction of analytical models of the ground, buildings, furniture and so on to simulate a situation during an earthquake disaster, and the authors construct an analytical model of the lifts. Since rope vibration is the main cause of earthquake damage to lifts,[1] the authors first constructed a seismic response analysis model of hoist ropes. This paper presents an overview of the earthquake-disaster digital twin, the analytical method and a seismic response analysis of the hoist rope vibration. The method of the vibration response analysis used in this paper is based on the wave equation and takes into account the spatial distribution and time variation of the tension on a rope.
2. Earthquake-Disaster Digital Twin
A digital twin is a technology that builds an accurate model in a virtual space that is identical to a structure in real space, almost like a twin. By monitoring and sensing information from the real structure using IoT technology in real-time, it is possible to build a highly accurate model in the virtual space. For example, when digital twins are applied to industrial facilities, simulations using digital twins can be useful for optimization, estimation of the effects of modifications of systems and so on. Digital twins can also be used to simulate accidents, malfunctions, disasters and so on, and the simulation results and knowledge gained can be fed back into the real space. Thus, the simulation results can be used for predictive maintenance, anomaly detection, business continuity planning, etc.
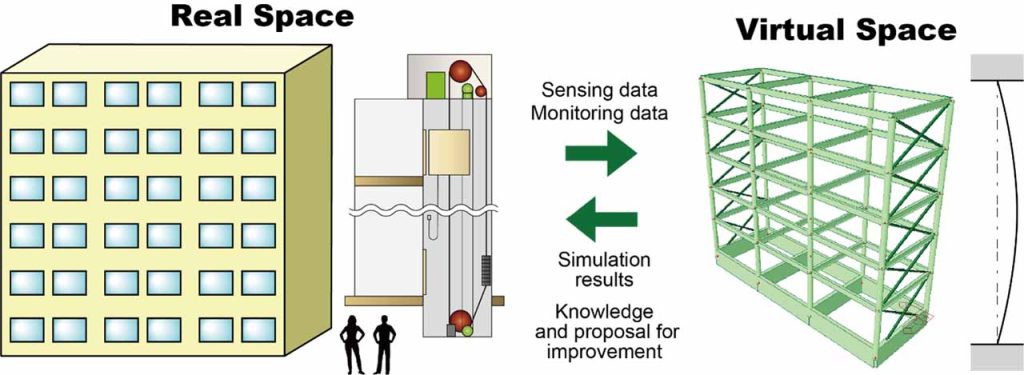
Utilizing this method, the authors’ research team is constructing an earthquake-disaster digital twin to predict and estimate the damage to condominium/apartment residential buildings during earthquakes.[3] Figure 1 shows a concept of the earthquake-disaster digital twin for a residential building. This earthquake-disaster digital twin of residential buildings includes earthquake ground motions, furniture, facilities, water, gas and electricity supply, lift, occupant behavior, etc. The behavior of an entire apartment building during an earthquake is simulated in a virtual space using the design information of the building or facilities in real space, the dynamic characteristics obtained from monitoring or sensing and the observed and estimated earthquake ground motions. The results and knowledge obtained from the simulation are useful for building consensus among residents on disaster prevention, creating and improving evacuation plans, disaster prevention plans and seismic reinforcement.
3. Analytical Methods of Rope Vibration
The authors are responsible for constructing an analytical model of a lift for the earthquake-disaster digital twin. In this paper, a vibration analysis model for hoist ropes, which is the main cause of earthquake damage to lifts, is constructed and a seismic response analysis is conducted.
The analytical method based on the wave equation[4] is applied for the digital twins of lifts. Considering the tension distribution due to the rope’s own weight and the tension variation due to the vertical motion of the car, the wave equation for the hoist ropes is shown in Equation (1).
As shown in Figure 2, t is the time, z is the spatial coordinate whose origin is the top of the building, u(z,t) is the transverse displacement of the rope, A is the linear density of the rope, V is the velocity of the cage and C is the damping coefficient of the rope. Assuming that the vertical elasticity of the rope is ignored, displacement of the car zcar is calculated geometrically as the following equation.
Where l is a length of the rope, ∆z is the length of each element of the rope in the finite difference method, N is the number of the rope elements and ui is the transverse displacement of the ith element of the rope. The vertical acceleration of the car zcar can be determined by the second-order derivative of zcar obtained from Equation (2), so tension is expressed as the following equation.
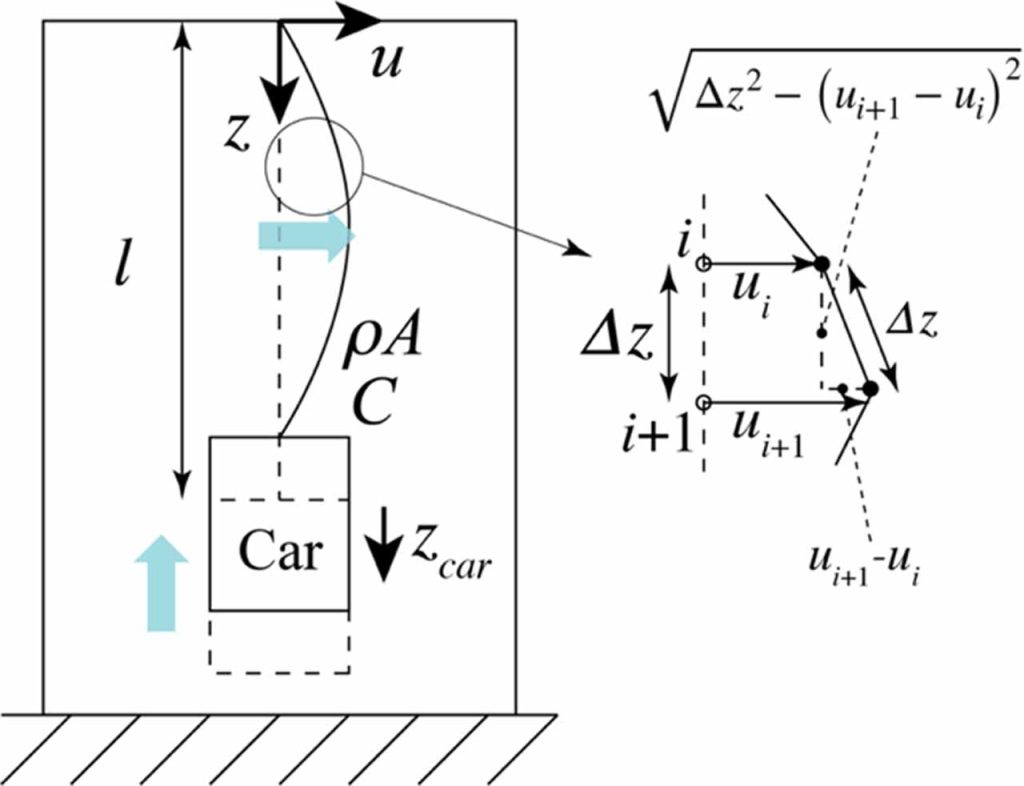
Where mcar1 is the mass of the car per rope, g is the gravitational acceleration.
For a more accurate simulation, the vertical elasticity of the rope and a connecting spring between the rope and the car should be considered. However, it has not been considered in this paper because it has nonlinear characteristics and increases the calculation time, and the simulation analysis in this paper is carried out for a large number of seismic waves. The influences of the vertical elasticity of the rope will be investigated in the future.
4. Seismic Response Analysis
4.1 Analytical Purpose
To confirm the effectiveness and clarify problems of the lift model for the earthquake-disaster digital twin of residential buildings, a seismic response analysis of a hoist rope of a lift in an apartment building was carried out.
4.2 Analytical Model
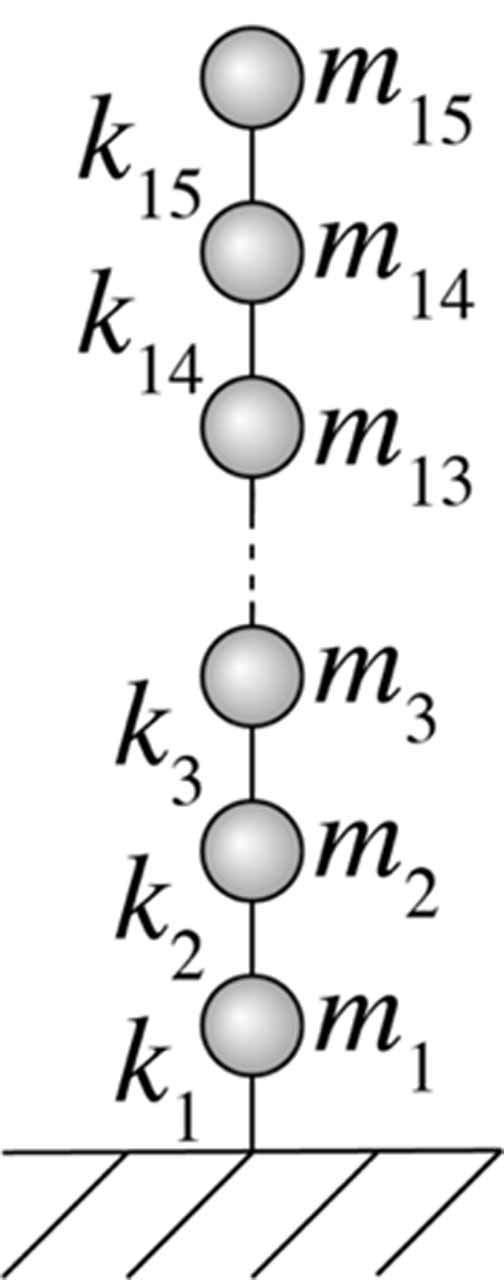
In this analysis, a lift in an apartment residential building was selected as an analytical target. This apartment residential building does not exist but is assumed to be located in the Japanese capital area. The building is a 15-story building with a height of 43.9 m, as shown in Figure 3 and Table 1. The mass and stiffness of each layer was assumed to be uniform.
| Mass of each story m₁, m₂, …, m₁₄, m₁₅ [kg] | 400000 |
| Stiffness of each story k₁, k₂, …, k₁₄, k₁₅ [N/m] | 2000 × 10⁶ |
| Height H [m] | 43.9 |
| 1st natural period Tₙ₁ [s] | 0.88 |
| Damping ratio ζ [%] | 3 |
Table 1:Parameters of the building model
| Mass of car mcar [kg] | 900, 1800 |
| Position of car | Ground, 5th, 8th story |
| Rope Length l [m] | 40.4, 29.1, 20.2 |
| Linear density ρA [kg/m] | 0.494 |
| Number of ropes | 4 |
| Roping of rope | 2:1 |
| Damping ratio ζ [%] | 0.2 |
Table 2: Parameters of the lift model
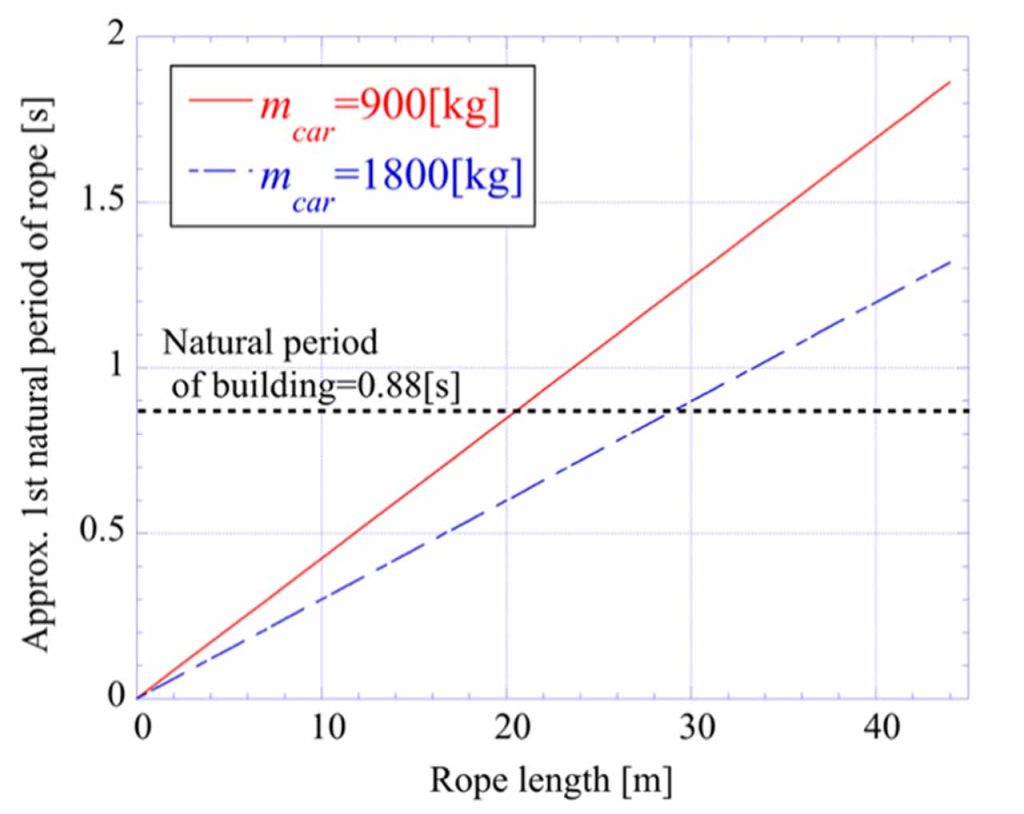
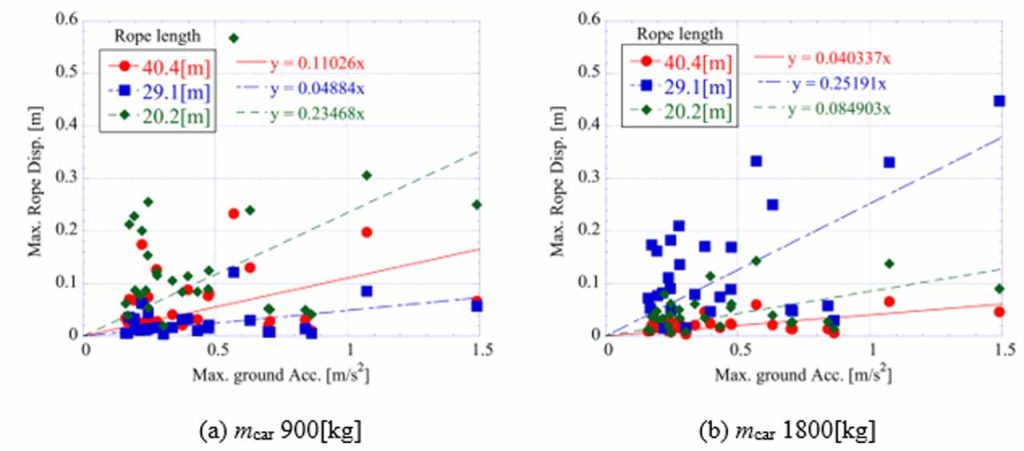
Table 2 shows the parameters of the lift. General lift specifications were used for the analysis. Two car masses were used, 900 kg and 1800 kg, taking into account the mass of the passengers inside. The approximate first natural period can be determined from the rope length. As shown in Figure 4, a rope length of 20.8 m for the car mass of 900 kg and a rope length of 29.4 m for the car mass of 1800 kg give the same natural period as that of the building. Therefore, the position of the car is selected in the fifth and eighth story, because the response increases when the natural period of the building is equal to that of the rope. In addition, the ground floor where the cars often stay was selected as the position of the car for comparison.
4.3 Analytical Procedure
First, the seismic response of the 15-story building was calculated, and then the response displacements of the building were input into the top and bottom parts of the rope.
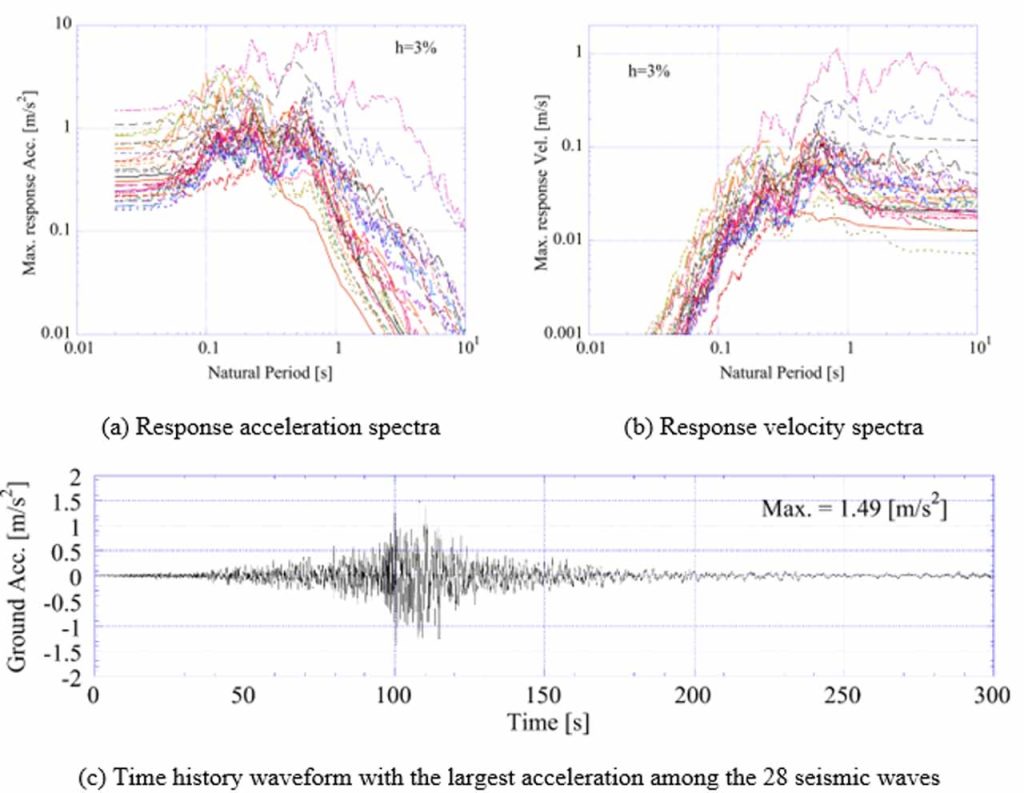
The seismic waves input to the building were a total of 28 horizontal waves observed by K-NET[5] at the same site in the Japanese capital area. The seismic waves used in the analysis have had JMA seismic intensity of 3.0 or higher since 2010. Figure 5 shows the properties of the seismic waves. Figures 5 (a) and (b) show the response spectra for all 28 seismic waves, and it is confirmed that the seismic waves have predominant periods of about 0.2 and 0.6 s. Figure 5 (c) is the time history waveform with the largest acceleration among the 28 seismic waves.
4.4 Analytical Results
Figure 6 shows the relationship between the maximum acceleration of each seismic wave and the maximum response displacement of the rope, together with the regression line. As the number of seismic waves is 28, there are 28 plots for each rope length. As shown in Figure 6, the response of the rope with a length of 20.2 m is larger when the mcar is 900 kg, and the response of the rope with a length of 29.1 m is larger when the mcar is 1800 kg. Therefore, the vibration of the rope becomes larger when the natural period of the building is equal to that of the rope. However, even when the conditions of the rope are the same, there are variations in the response displacement depending on the seismic wave. Therefore, it is important to accurately estimate the seismic waves and perform the seismic response analysis under conditions that increase the response of the ropes to create the earthquake-disaster digital twin. In the seismic response, the influence of nonlinearity due to tension variations expressed by Equation (3) is small,[4] so regression lines were applied. In the future, appropriate regression methods that are suitable for nonlinear phenomena will be investigated, and a probabilistic approach that can account for response variations will be applied for accurate evaluations.
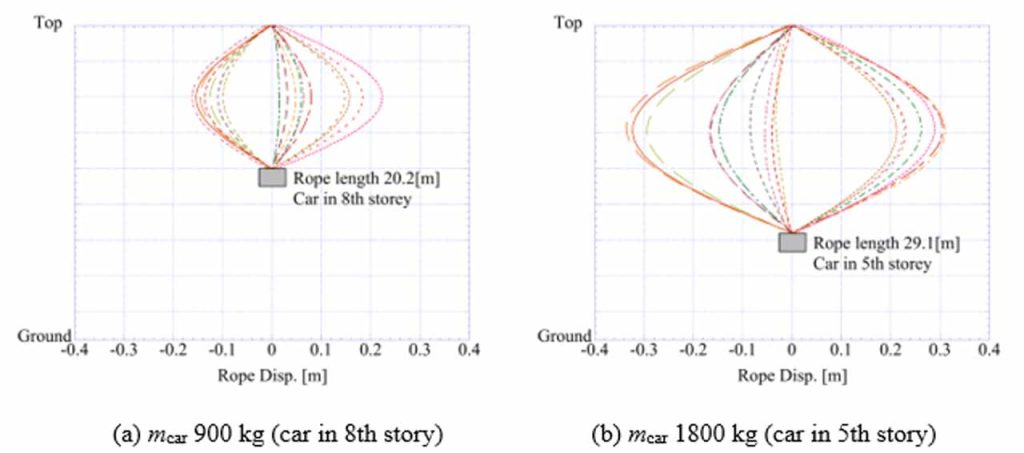
Figure 7 shows the vibration mode of the ropes for the seismic wave with the largest acceleration among the 28 seismic waves. From Figure 7, it is confirmed that the first vibration mode is dominant because the first natural period of the building and that of the rope are close. In addition, the first vibration mode will be the evaluation target for the earthquake-disaster digital twin, because the response displacement of the 1st vibration mode is generally larger than the other higher modes.
5. Conclusion
In this paper, the authors introduced the earthquake-disaster digital twin for apartment residential buildings with lifts and constructed the analysis model of hoist ropes. As a result of the seismic response analysis of the hoist rope, the following effectiveness and issues were confirmed.
The vibration analysis method and model of hoist ropes of lifts for the earthquake-disaster digital twin are effective for evaluating the behavior of the ropes during earthquakes. However, a seismic experiment using a shaker table of an actual lift system in a building is required to improve the accuracy of the analytical method and model in the future.
Even if the conditions of the building and the rope are the same, the response of the ropes will be different depending on the seismic wave. Therefore, an accurate estimation of the seismic waves is very important to predict the damage to a lift caused by an earthquake. In addition, seismic response analysis for different types of seismic waves is also necessary, because even if the seismic waves are small, the response of the rope may be large depending on the frequency characteristics of the seismic waves.
In the future, an investigation regarding the conditions under which the response of the rope does not increase during earthquakes, an investigation regarding the influence of the vertical elasticity of the rope and so on and an investigation regarding regression methods and probabilistic approaches for the rope responses will be carried out.
Acknowledgements
This work was supported by JST-Mirai Program Grant Number JPMJMI22H2, Japan. The authors would like to express their appreciation to JST and the members of our research team for their valuable advice and devoted assistance in conducting this project.
References
[1] S. Fujita, M. Shimoaki, and K. Minagawa, “Report on Seismic Damage of Lifts and Escalators by Large Earthquakes in Japan”. Transportation Systems in Buildings, Vol 3, No 1 (2020).
[2] Statistics Bureau, Japan Ministry of Internal Affairs and Communications, 2018 Housing and Land Survey, stat.go.jp/data/jyutaku/2018/pdf/g_gaiyou.pdf, (2018), in Japanese.
[3] T. Horiuchi, K. Kajiwara, Y. Sekimoto, H. Koizumi, S. Fujita and K. Minagawa, “Construction of an Earthquake-Disaster Digital Twin of Condominium/Apartment Residential Buildings.” Proceedings of the 16th Japan Earthquake Engineering Symposium, Day1-G404-22.pdf (2023), in Japanese.
[4] K. Minagawa and S. Fujita, “Activities and Results of the Rope Vibration Analysis Working Group in the Japan Society of Mechanical Engineers.” Proceedings of the 14th Symposium on Lift & Escalator Technologies, pp. 13-1 – 13-10 (2023).
[5] National Research Institute for Earth Science and Disaster Resilience, Strong-motion Seismograph Networks, kyoshin.bosai.go.jp
Get more of Elevator World. Sign up for our free e-newsletter.